Damian Conway

The first task of the 18th Weekly Challenge was to find the longest common substring(s) in a set of strings. That is, given a set of strings like “ABABC”, “BABCA” and “ABCBA”, print out “ABC”.

The “best practice” solution is a technique known as suffix trees, which requires some moderately complex coding. However, we can get very reasonable performance for strings up to hundreds of thousands of characters long using a much simpler approach.

Let’s start with a very concise, but suboptimal, solution. If we has a list of all the possible substrings for each string:

ABABC: ABABC, ABAB, BABC, ABA, BAB, ABC, AB, BA, BC, A, B, C
BABCA: BABCA, BABC, ABCA, BAB, ABC, BCA, BA, AB, BC, CA, B, A, C
ABCBA: ABCBA, ABCB, BCBA, ABC, BCB, CBA, AB, BC, CB, BA, A, B, C

...then we could treat each list as a set, take the intersection of those sets:

ABC, AB, BA, BC, A, B, C

...then simply find the longest element: ABC

Of course, sometimes the intersection of all possible substrings will have more than one longest element:

SHAMELESSLY
NAMELESS
LAMENESS

...so we need to ensure that our algorithm finds them all.

Given that Raku has sets and set operations built right into the language, the only challenge here is to generate the full set of all possible substrings for each string. And, given that Raku has very sophisticated regular expression matching, that’s no real challenge either.

In a normal regex match:

   my $str = '_ABC_ABCBA_';

   say $str.match(/ <[ABC]>+ /);
   # Says: ｢ABC｣

The string is searched for the first substring that matches the pattern: in the above example, the first sequence of one or more of 'A', 'B', or 'C'. But we can also ask the Raku regex engine to return every separate substring that matches, by adding a :g (or :global) adverb:

say $str.match(/ <[ABC]>+ /, :g);
# Says: ( ｢ABC｣ ｢ABCBA｣ )

Or we can ask for every overlapping substring that matches, by adding an :ov
(or :overlap) adverb:

say $str.match(/ <[ABC]>+ /, :ov);
# Says: ( ｢ABC｣ ｢BC｣ ｢C｣ ｢ABCBA｣ ｢BCBA｣ ｢CBA｣ ｢BA｣ ｢A｣ )

Or we can ask for every possible substring that matches, by adding an :ex
(or :exhaustive) adverb:

say $str.match(/ <[ABC]>+ /, :ex);
# Says: ( ｢ABC｣ ｢AB｣ ｢A｣ ｢BC｣ ｢B｣ ｢C｣
# ｢ABCBA｣ ｢ABCB｣ ｢ABC｣ ｢AB｣ ｢A｣
# ｢BCBA｣ ｢BCB｣ ｢BC｣ ｢B｣
# ｢CBA｣ ｢CB｣ ｢C｣ ｢BA｣ ｢B｣ ｢A｣ )

And, of course, this last alternative is precisely what we need: a way to extract every possible substring of a string. Except that we need to find substrings containing all possible characters, not just A/B/C, so we need to match against the “match anything” dot metacharacter:

say $str.match(/ .+ /, :ex);
# Says: ( ｢_ABC_ABCBA_｣ ｢_ABC_ABCBA｣ ｢_ABC_ABCB｣
# ｢_ABC_ABC｣ ｢_ABC_AB｣ ｢_ABC_A｣)
# ...(54 more elements here)...
# ｢BA_｣ ｢BA｣ ｢B｣ ｢A_｣ ｢A｣ ｢_｣ )

As the above example illustrates, these regex matches return a sequence of Match objects (denoted by ｢...｣ brackets on output), rather than a list of strings. But such objects are easy to convert to a list of strings, by calling the string coercion method on each of them (using a vector method call: ».):

say $str.match(/ .+ /, :ex)».Str;
# Says: ( _ABC_ABCBA_ _ABC_ABCBA _ABC_ABCB
# _ABC_ABC _ABC_AB _ABC_A
# ...(54 more elements here)...
# BA_ BA B A_ A _ )

To find the common substrings of two or more strings, we need the exhaustive list of substrings for each of them. If the strings are stored in an array, we can use another vector method call (».) on that array to perform the same substring-ification on each of the strings:

@strings».match(/.+/, :ex)».Str

Now we just need to treat each of the resulting lists as a set, and take the intersection of them. That’s easy because Raku has a built-in ∩ operator, which we could use to reduce all the lists to a single intersection, like so:

[∩] @strings».match(/.+/, :ex)».Str

To extract a list of substrings from this set, we simple ask for its keys:

keys [∩] @strings».match(/.+/, :ex)».Str

We now have a list of the common substrings, so we just need a way to find the longest substring(s) in that set. Raku has a built-in max function, but that would only find the first substring of maximal length. We need all of them.

To get them, we’ll augment the existing built-in function with a new variant; one that returns every maximal value, not just the first. This new subroutine takes the same arguments as the existing max builtin, but requires an extra :all adverb, to indicate that we want all the maxima:

   # "Exhaustive" maximal...
   multi max (:&by = {$_}, :$all!, *@list) {
       # Find the maximal value...
       my $max = max my @values = @list.map: &by;

       # Extract and return all values matching the maximal...
       @list[ @values.kv.map: {$^index unless $^value cmp $max} ];
   }

Now we can keep just the longest common substrings (i.e. those substrings whose .chars value is maximal) like so

max :all, :by{.chars}, keys [∩] @strings».match(/.+/, :ex)».Str

The original challenge specification requires that the program accept a list of strings as command-line arguments, and prints their longest common substrings, which looks like this:

   sub MAIN (*@strings) {
       .say for
           max :all, :by{.chars},
                keys [∩] @strings».match(/.+/, :ex)».Str
   }

Problem solved!

Except for those pesky bioinformaticists. Give them this solution and they’ll immediately look for the longest common substrings in half a dozen DNA sequences with ten thousand base pairs. And instantly discover the fundamental flaw in this approach: that the number of possible substrings in a string of length N is (N²+N)/2, so the costs of computing and storing them quickly become prohibitive.

For example, to find the longest common substrings of six 10000-base DNA strings, we’d need to extract and refine just over 300 million substrings. That quickly becomes inpractical, especially when the bioinformaticists decide that they’re more interested in DNA strands with hundreds of thousands of base pairs, at which point the initial exhaustive lists of substrings now have at least 30 billion elements collectively. We clearly need a more scalable approach.

Fortunately, it’s not hard to devise one. The number of substrings of any length in a N-character string is O(N²), but the number of substrings of a specific length M is only N-M+1. For example in a 10-character string like "0123456789", there are only six 5-character substrings: "01234", "12345", "23456", "34567", "45678", and "56789".

So, if we knew in advance how long the longest common substring was going to be
(i.e. the optimal value of M), we could generate and compare only substrings of that
exact length (/. ** {$M}/), using :ov overlapping pattern matching
(instead of :ex exhaustive):

@strings».match(/. ** {M}/, :ov)».Str

That would reduce the computational complexity of the algorithm to a far more scalable O(N).

Of course, initially we have no clue how long the longest common substring is going to be (except that it must be between 1 and N characters long). So we do what all good computer scientists do in such situations: we guess. But good computer scientists don’t like to call it “guessing”; that doesn’t sound scientific at all. So they have a fancy formal name for this approach: the Binary-Chop Search Algorithm.

In a binary search, we start with some kind of reasonable upper and lower bounds
of the optimal substring length we’re seeking ($min and $max). At each step,
we compute our “guess” of that optimal length ($M) by averaging those two bounds
($M = round ($min+$max)/2), then somehow check whether our guess was correct:
in this case, by checking if the strings do in fact have any common sunstrings of length $M.

If the guess is too small, then the optimal substring length must be bigger, so the guess becomes our new lower bound ($min = $M + 1). Similarly, if the guess is too high, then it becomes our new upper bound ($max = $M - 1). We repeat this guessing process, halving the search interval at each step, until we either guess correctly, or else run out of candidates...which occurs when the updated value of $min eventually exceeds the updated value of $max.

Because a binary-chop search halves the search interval at each step, the complete search always requires O(log N) guesses in the worst case, so if we check each guess using our O(N) fixed-length common substring computation, we’ll end up with an O(N log N) algorithm for finding the longest common substring.

Which looks like this:

   sub lcs (@strings) {
       # Initial bounds are 1 to length of shortest string...
       my ($min, $max) = (1, @strings».chars.min);

       # No substrings found yet...
       my @substrs;

       # Search until out-of-bounds...
       while $min ≤ $max {
           # Next guess for length of longest common substring...
           my $M = round ($min+$max)/2;

           # Did we find any common substrings of that length???
           if [∩] @strings».match(/. ** {$M}/,:ov)».Str -> $found {
               # If so, remember them, and raise the lower bound...
               @substrs = $found.keys;
               $min = $M+1;
           }
           else {
               # Otherwise, lower the upper bound...
               $max = $M-1;
           }
       }

       # Return longest substrings found...
       return @substrs;
   }

That’s ten times as much code to achieve exactly the same result, but with it we also achieved a considerable improvement in performance. The one-liner solution takes just under 90 seconds to find the longest common substrings from six 1000-character strings; the binary-chop solution finds the same answer in 1.27 seconds. The general performance of the two solutions looks like this:

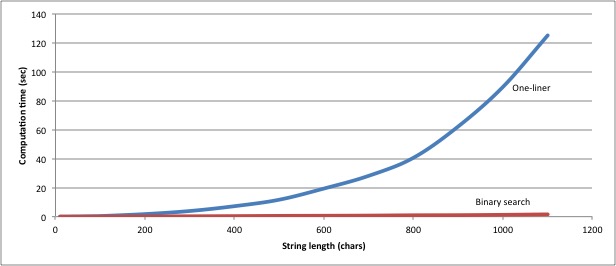
More importantly, at about 1000 characters per string, the one-liner starts failing
(possibly due to memory issues), whereas the binary-chop version has no problem
up to 10000-character strings.

Except that, at that point, the binary chop solution is taking nearly a minute to find the common substrings. Time to optimize our optimization.

The slow-down on longer string lengths seems mostly to be coming from the use of a regex to break the string into overlapping M-character substrings on each iteration. Regexes in Raku are immensely powerful, but they are still being internally optimized, so they’re not yet as fast as (say) Perl regexes.

More significantly, Raku regexes have a fundamental performance limitation in a situation like this: each result from the match has to be returned in a full Match object, which then has to be converted back to a regular Str object. That greatly increases the time and space required to run the algorithm.

But if we could work directly with strings we’d save most of the space, and a great deal of the time spent in constructing and transforming Match objects. And, in this case, that’s easy to do...because all we need at each search step is to construct a list of overlapping substrings of a fixed length $M:

   "ABCDEFGH"           # $str

   "ABCDE"              # $str.substr(0,$M)
    "BCDEF"             # $str.substr(1,$M)
     "CDEFG"            # $str.substr(2,$M)
      "DEFGH"           # $str.substr(3,$M)

In other words, for each string, we just need to construct:

   # For each offset, start at offset, take substring of length M
   (0..$str.chars-$M).map(-> $offset { $str.substr($offset, $M) })

...which, for all the strings is just:

   # For each string...
   @strings.map(-> $str {
       # Build a list of substrings at each offset...
       (0..$str.chars-$M).map(-> $offset {$str.substr($offset,$M)})
   })

Or we could write it more compactly, using the topic variable $_ instead of $str,
and a placeholder variable $^i instead of $offset:

   @strings.map:{(0 .. .chars-$M).map:{.substr($^i,$M)}}

Using that expression to replace the overlapping regex match, and tidying the binary search loop by using internal state variables instead of external my variables, we get:

   sub lcs (@strings) {
      # Search...
      loop {
         # Bounds initially 1 to length of shortest string...
         state ($min, $max) = (1, @strings».chars.min);

         # When out-of-bounds, return longest substrings...
         return state @substrs if $max < $min;

         # Next guess for length of longest common substring...
         my $M = round ($min+$max)/2;

         # Did we find common substrings of that length???
         if [∩] @strings.map:{(0.. .chars-$M).map:{.substr($^i,$M)}}
         {
             # If so, remember them, and increase the lower bound...
             @substrs = $^found.keys;
             $min = $M+1;
         }
         else {
             # Otherwise, reduce the upper bound...
             $max = $M-1;
         }
      }
   }

Changing the way we extract candidate substrings provides another considerable boost in performance. Whereas the regex-based version took 54.6 seconds to find the longest common substring of six 10000-character strings, this new substring-based version finds the same answer in 3.1 seconds. And our new version scales much better too:

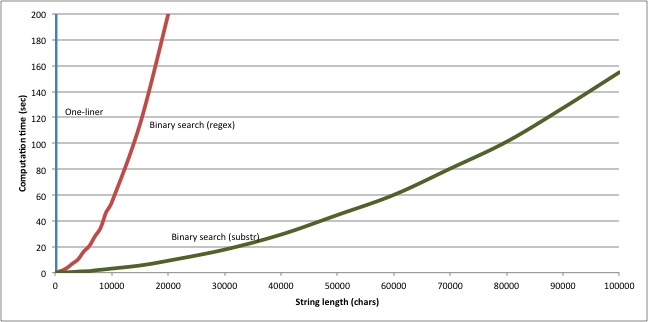
Which just goes to show: no matter how cool and powerful your programming language is, no matter how much it lets you achieve in a cunning one-liner, when it comes to scalable performance, nothing beats the right algorithm.

Damian