Damian Conway

The first task of the 15th Weekly Challenge was to find the optimal position in the line for dessert.

This is a reformulation of the old conundrum of creating buggy whips or cowboy movies or physical book stores or carbon-based energy sources: when is the best time to opt in for an ever-increasing slice of an ever-diminishing pie?

In this task, the pie is big enough for 100 people, but the first person in line gets a slice equivalent to only 1% of it. The second person gets 2% of what’s left, the third gets 3% of what remains after that, et cetera, et cetera, until the one-hundredth person receives 100% of whatever crumbs are left after the preceding ninety-nine have taken their share. In other words, we’re “Making Apple-pie Great Again!”

The actual task is to determine which is the optimal position in the line. Is it better to get in early and get a small slice of a still-large pie? Or to wait and eventually obtain a bigger slice of the leftovers? Let’s answer that question six different ways.

1. Imperative slices

I started my developer career as a C programmer and I still find it natural to approach small problems like this one in an imperative mode. So my very first attempt to answer the question (mercifully, in Raku rather than in C) looked like this:

    # Start with a full pie, and no idea who gets the most...
    my $pie       = 1.00;    # i.e. 100%
    my $max-share = 0.00;    # i.e.   0%
    my $max-index;

    # For everyone in line...
    for 1..100 -> $N {

        # Take N% of what’s left as the next share...
        my $share = $pie * $N/100;
        $pie -= $share;

        # Remember it if it’s maximal...
        if $share > $max-share {
            ($max-index, $max-share) = ($N, $share);
        }
    }

    # Report the biggest share taken...
    say "$max-index => $max-share";

It’s not pretty, nor concise, nor simple, but it’s quick and it produces an answer:

    10 => 0.06281565095552947

In other words, the optimal place in line is to be tenth, which secures you just over 6¼ percent of the original pie.

But this solution has some problems...and not just the obvious ones of gawkiness, prolixity, and far too many moving parts. The deeper issue is that it makes an significant unwarranted assumption (one that happens to be correct, though that’s no excuse as I didn’t know it at the time).

So let’s set about improving the solution.

The unwarranted assumption I made was that there actually was a single optional place in the queue. But what if there were two equally good places? Or three? Or a plateau after which all places were equally good? The code above actually only tells us that the person in tenth place is the first person who receives a maximal share. What if there were others?

It’s also a red flag that we’re identifying that first maximal value “manually”, by checking each new share as we create it within the loop. Raku has a perfectly good built-in max function that could do that for us. Though, of course, what we really need is a max function that returns all the places where the maximum is found, not just the first. Well...Raku has that too: maxpairs

Yet another red flag in the code is the need to add comments documenting the various numbers representing percentages. (e.g. 1.00 and $N/100). There ought to be a way to have the code itself make that obvious.

Here’s my second attempt at an imperative solution, incorporating all those improvements:

    # Add a percentage operator...
    sub postfix:<%> (Numeric $x) { $x / 100 }

    # Start with 100% of the pie, and no shares yet...
    my $pie = 100%;
    my %share;

    # For everyone in line...
    for 1..100 -> $N {
        # Remove a share for the Nth person from the pie...
        $pie -= ( %share{$N} = $pie * $N% );
    }

    # Finally, report the share(s) with maximal values...
    say %share.maxpairs;

Surprisingly, Raku doesn’t have a “percentage” operator built in. Well, perhaps it’s not so surprising, given that it already uses the % symbol as a prefix sigil, an infix operator, an infix regex metaoperator, and a nameless static variable. Adding a permanent fifth meaning to that single character might not greatly improve overall code clarity.

Except that, here, it definitely does. Which is why Raku makes it trivially easy to add a postfix % operator that simply divides its numeric argument by 100:

    sub postfix:<%> (Numeric $x) { $x / 100 }

So now we can just write:

$pie = 100%

and:

%share{$N} = $pie * $N%

without needing comments to explain that they're percentages.

And because we’re storing each computed share in a hash table, we can use the built-in .maxpairs method to retrieve a list of all the entries of %share with maximal values. Printing out that list, we find it contains only a single pair:

    (10 => 0.06281565095552947)

...thereby confirming that the tenth person in line is the only one who achieves optimal pie.

2. Stateful pie

That second impertaive version is 33% shorter and probably 33% more readable, but it still has some issues. For example, any time I see a variable like %shares that exists only to be populated in a for loop and then used exactly once afterwards, I get twitchy. And then I reach for a gather/take:

    say maxpairs gather for 1..100 -> $N {
        state $pie = 100%;
        $pie -=  my $share = $pie * $N%;
        take $N => $share;
    }

In this version we’ve moved the $pie variable inside the loop, declaring it as a (persistent) state variable instead of a (transient) my variable. We still compute N% of the remaining pie on each iteration, but now we take that value, along with the current value of N, as a pair: take $N => $share

This means that, after the loop terminates, the gather will return a list of pairs whose keys are the positions in line, and whose values are the respective shares of the pie.

Once the loop terminates and the gather returns the list of pairs, we just need to filter out the maximal shares. Surprisingly, Raku doesn’t offer a suitable maxpairs built-in function (only the .maxpairs method on hashes), but fortunately Raku makes it easy to build a very powerful one that will handle everything we’re going to throw at it in the rest of this exploration:

  # Maximal values from a list of pairs...
  multi maxpairs (@list where @list.all ~~ Pair, :&by = {$_}) {
      my $max = max my @values = @list».value.map: &by;
      @list[ @values.pairs.map: {.key unless .value cmp $max} ];
  }

  # Maximal values extracted from a list of containers...
  constant Container = Iterable | Associative;
  multi maxpairs (@list where @list.all ~~ Container, :&by!) {
      my $max = max my @values = @list.map: &by;
      @list[ @values.pairs.map: {.key unless .value cmp $max} ] :p;
  }

  # Maximal values directly from a list of anything else...
  multi maxpairs (:&by = {$_}, *@list) {
      my $max = max my @values = @list.map: &by;
      @list[ @values.pairs.map: {.key unless .value cmp $max} ] :p;
  }

There are three multiply dispatched versions of the function because we need to process various types of lists slightly differently. Nevertheless, in each case, we first extract the actual values we'll be maximizing by (my @values = @list.map: &by), then find the maximum of those values (my $max = max my @values), then then we find the indices of every list element with that maximal value (.key unless .value cmp $max), and finally return the elements at those indices, as a list of pairs (@list[...] :p).

With that function now “built in”, we can immediately identify and print the list of every maximal pair gathered in the loop: say maxpairs gather for 1..100 {...}

3. Sequential pie

Whenever I realise that I'm using a gather to generate a sequence of values in Raku, I immediately wonder whether I could do so more easily with the ... sequence generation operator. This operator is especially well adapted to building new values from previous values, which is exactly what we’re doing here: progressively reducing the pie as we progressively increase the percentages we’re handing out.

The ... operator has three components: an initial value, some code for building the next value from the previous, and a terminating condition. In this case, our initial condition is just that we have a full pie, and no-one has yet been given a share of it:

    hash( pie => 100%, N => 0, share => 0% )

To build a new value from the previous one, we simply increment N, then build a new hash in which N is given its updated value, a new share of N% is allocated, and the pie itself is diminished by that share (by reducing it to (100-N)%). That is:

sub next-share (\previous) {
given previous<N> + 1 -> \N {
return hash
N => N,
share => previous<pie> * N%
pie => previous<pie> * (100 - N)%,
}
}

Then we can build our list of shares:

constant shares
= hash(pie=>100%, N=>0, share=>0%), &next-share ... *;

Note that our terminating condition is * (“Whatever, dude!”), so this is actually a lazily evaluated infinite list. But we’re only interested in the first 101 values (i.e. from N=>0 to N=>100), so we extract those and then find the maximal pair(s), using each element’s share value to compare them:

    say maxpairs :by{.<share>}, shares[^100];

Notice how far we have now come from the original iterative solution. This approach more-or-less just describes what we want. We simply state the initial condition and describe how the values change. Then we ask for the specific information we require: Show us the maximum of the pairs, sorted by share, from the first 100 shares.

Both solutions require about the same amount of code, but this one is far less likely to include algorithmic mistakes, computational errors, or out-by-one problems. It doesn’t even require any variables to get the job done.

4. Functional pie

And, speaking of not requiring any variables, what about a pure functional solution?

Well that’s easy too. We just use the classic recursive list generation pattern:

To return a list of shares of the remaining pie...
With the next share (i.e. N% of what’s left)...
Return that share and its position in the list
Plus the list of shares of the remaining pie
(Provided there’s still any pie left to share)

Which, translated line-for-line into Raku, looks like this:

    sub shares (\pie = 100%, \N = 1) {
        given N% * pie -> \share {
            pair(N, share),
            |shares( pie - share, N+1)
                if 1% <= share <= 100%
        }
    }

Or, if you prefer your recursive and base cases better distinguished:

    # Recursive definition of shares list...
    multi shares (\pie = 100%, \N = 1) {
        given pie * N% -> \share {
            pair(N, share), |shares(pie - share, N+1)
        }
    }

    # Base case returns an empty list...
    multi shares (\pie, \N where N > 100) { Empty }

Either way, once we generate the complete list of shares, we just need to extract the maximal pair(s) from that list:

    say maxpairs shares();

5. Mathematical pie

A few days after I completed that flurry of code evolutions, I woke up one morning chagrined by the realization that I’d missed an “utterly obvious” solution.

I thought about the pattern of percentages allocated to each person in line; how they increased linearly:

    1%, 2%, 3%, 4%, ...

And then I though about how much pie was still available at any point, and how it decreased not linearly, but exponentially (because taking each share decreases the pie by N% of what's left, not by N% of the original pie):

    100%,  100%×99%,  100%×99%×98%,  100%×99%×98%×97%, ...

If I had those two complete lists (successive share percentages and progressive pie remains), then I could just multiple each of the corresponding elements together to find out how much each person in line would receive:

     1%,     2%,           3%,             4%, ...
      ×       ×             ×               ×
    100%,  100%×99%,  100%×99%×98%,  100%×99%×98%×97%, ...

Creating a list of the linearly increasing percentages is trivial in Raku:

    (1%, 2% ... 100%)

And creating a list of exponentially decreasing leftovers is hardly any more difficult:

    [\*] (100%, 99% ... 1%)

The [\*] operator produces a list of the partial products from successive multiplication of the elements in percentages list. In other words, it multiplies the first two elements, and then the first three, and then the first four, et cetera, until it’s produced a list of all of the partial products. So we get:

    100%, (100% * 99%), (100% * 99% * 98%) ...

Given those two lists, we can simply multiple each percentage by each corresponding leftover amount, using vector multiplication:

(1%, 2% ... 100%) »*« [\*] (100%, 99% ... 1%)

...giving us a list of who got how much pie. Then we can just filter that list for the maximal index/pie-share pair:

    say maxpairs (1%, 2%...100%)  »*«  [\*] (100%, 99%...1%);

And there’s our answer once again...now in a single line.

6. Visual pie

Of course, every one of these solutions has relied on us having that very handy maxpairs function, to search through the outcomes and locate the optional place in line.

If we didn’t have that function, or any other “find the maximum” function, we could still eyeball the answer, if only we could see what the data looks like.

Well, that’s easy in Raku too, thanks to a lovely pair of modules created by Moritz Lenz:

    use SVG;
    use SVG::Plot;

    # Work out the shares, as before...
    constant shares = (1%, 2% ... 100%) »*« [\*] (100%, 99% ... 1%);

    # Plot the data and write it to an SVG file...
    spurt 'chart.svg'.IO,
        SVG.serialize:
            SVG::Plot.new(
                title  => 'Percentage shares of the pie',
                values => [shares »*» 100,],
                x      => [0..100],
            ).plot(:xy-lines);

    # Take a look...
    shell 'open chart.svg';

...which generates and displays the following graph:

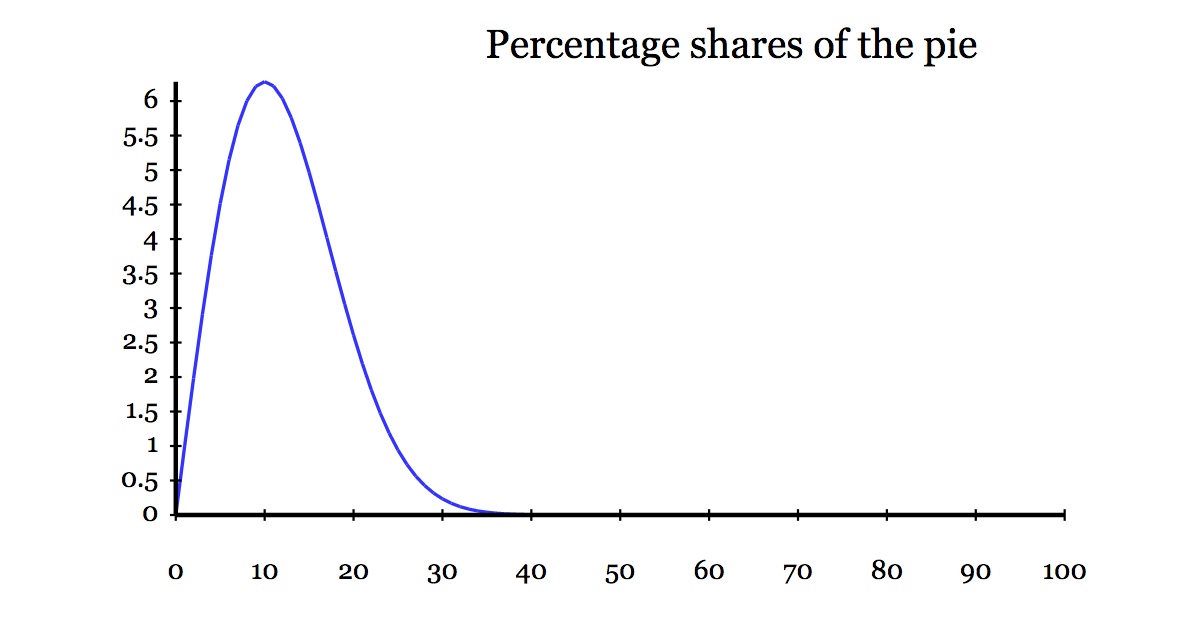
...which, at a glance, tells us that person number 10 is still getting the best deal, with just over 6% of the pie.

So, no matter whether you prefer to slice your pies imperatively, statefully, declaratively, functionally, mathematically, or visually, Raku makes it easy write code that works in the way you are most comfortable thinking.

And that’s important...whether it’s something as simple as letting you seamlessly add a missing built-in like % or maxpairs, or something as convenient as generating complex sequences and then applying vector arithmetic between them, or something as profound as allowing you to code fluently in whichever programming paradigm helps you to reason about problems most effectively.

Because people shouldn’t have to adapt to the needs of programming languages;
programming languages should adapt to the needs of people.

Damian