Dana Jacobsen

Math::Prime::Util, and the optional Math::Prime::Util::GMP back end, are a set of modules for number theory in Perl, with a large overlap of functionality with PARI/GP. This is an update on some of the things that were new in the April release (0.40 of MPU, 0.19 of MPU::GMP).

The usual speed improvements in various areas, some approximation improvements, and new functions. Primality testing benchmarks also show Perl has state of the art solutions.

New functions:

• twin_prime_count and nth_twin_prime, similar to the regular prime_count and nth_prime functions, give the count or value for twin primes.


• twin_prime_count_approx and nth_twin_prime_approx, also similar to the standard functions, give fast approximations, which are especially useful for very large inputs.


• random_shawe_taylor_prime generates random proven primes using the FIPS 186-4 method. A ..._with_cert version is also available that returns a primality certificate. This is somewhat faster than the random Maurer primes, but returns a smaller subset, so is not used for the generic random_proven_prime function. It's nice to have if one wants FIPS behavior.
  
• GMP versions of is_power and exp_mangoldt, so these run faster for large inputs.

Some other improvements include a more accurate nth_prime_approx (using an inverse Riemann R function instead of the Cipolla approximation), and small speedups in a number of functions.

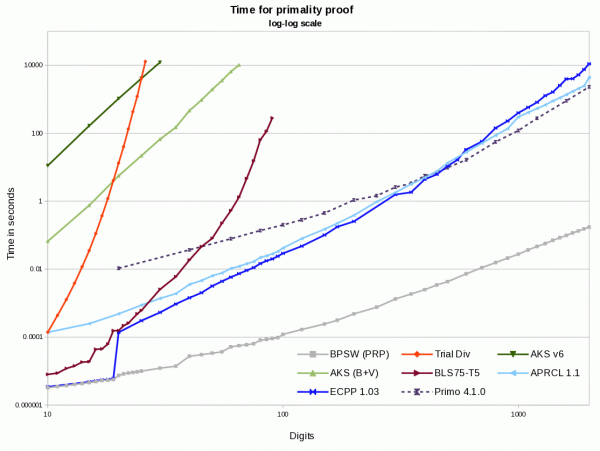
Two big speedups in GMP primality tests. ECPP has updated polynomial data and some performance updates to keep its lead as the fastest open source primality proof for up to 500 digits. It remains competitive with Pari and the newest mpz_aprcl for quite a while after. With the larger poly set doesn't do too bad compared with Primo up to 2000 digits.

AKS has an improved algorithm using changes from Bernstein and Voloch, with a nice r/s heuristic from Bornemann. It runs about 200x faster now, making it, by quite a bit, the fastest publicly available AKS implementation. Even this updated version is still millions of times slower than ECPP. Repeat after me: AKS is important for the theory, but is not a practical algorithm...

Shows primality timing measurements for a number of open source solutions. All but APRCL and Primo are included in Math::Prime::Util.