Perl Weekly Challenge # 18: Priority Queues and Binary Heaps In Perl 6
In this previous blog post, I provided some answers to the Week 18 of the Perl Weekly Challenge organized by Mohammad S. Anwar.
However, I omitted the Perl 6 solution to the priority queues part of the challenge, because I wanted to use a binary heap to solve it, and this required too many explanations: the blog post was just getting too long. So this post will complete the previous post and look into binary heaps in Perl 6.
Spoiler Alert: This weekly challenge deadline is due in several days from now (July 28, 2019). This blog post offers some solutions to this challenge, please don't read on if you intend to complete the challenge on your own.
This part of the challenge goes like this:
Write a script to implement Priority Queue. It is like regular queue except each element has a priority associated with it. In a priority queue, an element with high priority is served before an element with low priority. Please check this wiki page for more information. It should serve the following operations:
1) is_empty: check whether the queue has no elements.
2) insertwithpriority: add an element to the queue with an associated priority.
3) pullhighestpriority_element: remove the element from the queue that has the highest priority, and return it. If two elements have the same priority, then return element added first.
As already explained in my previous post, there are numerous ways to design simple priority queues (at least when performance is not an issue, for instance if the data set isn't very large). For example, it might be sufficient to maintain an array of arrays (AoA), where each of the arrays is a pair containing the item and associated priority. Or an array of hashes (AoH) based on the same idea. This means that each time we want to pull the highest priority element, we need to traverse the whole data structure to find the item with the highest priority. This may be quite slow when there are many items, but this may not matter if our data structure only has a few dozen items.
Another way is to build a hash of arrays (HoA), where the hash keys are the priorities and the hash values are references to arrays. When the number of priorities is relatively small (compared to the number of items in the queues), this tends to be more efficient, but note that we still need to traverse the keys of the hash until we find the highest priority. An AoA with the index being the priority and the sub-hashes the item might be more efficient (because the priorities remain sorted), but this requires the priorities to be relatively small positive integers. We still have to traverse the top data structure until we find the first non-empty sub-array. We used this data structure for our Perl 5 implementation and can translate our P5 code into Perl 6 as follows:
use v6;
sub new-queue {
my @queue; # an AoA
sub is_empty {
for @queue -> $item {
next unless defined $item;
return False if $item.elems > 0;
}
True;
}
sub insert_with_prio ($item, Int $prio) {
push @queue[$prio], $item;
}
sub pull_highest_prio {
for reverse @queue -> $item {
next unless defined $item;
return shift $item if $item.elems > 0;
}
}
return &is_empty, &insert_with_prio, &pull_highest_prio;
}
my (&is-empty, &insert, &pull-prio) = new-queue;
# Testing the above code
for 1..20 -> $num {
insert($num,
$num %% 10 ?? 10 !!
$num %% 5 ?? 5 !!
$num %% 3 ?? 3 !!
$num %% 2 ?? 2 !!
1);
}
for 1..20 -> $num {
say pull-prio;
}
say "Empty queue" if is-empty();
As in the P5 version, we're using functional programming to implement a pseudo-object system, in which the new-queue subroutine is acting as an object constructor, although it is implemented as a function factory. The @queue object is limited to the scope of the new-queue constructor, but the three methods returned to the caller are closures that can access to the content of their shared object, @queue. Please refer to the other blog post mentioned above for further details on this implementation and on the test code at the end. This script displays more or less the same as the P5 implementation:
$ perl6 queues.p6
10
20
5
15
3
6
9
12
18
2
4
8
14
16
1
7
11
13
17
19
Empty queue
Another possibility is to use a heap, a data structure that usually has better performance (when it matters). This what we will look into now.
Background on Binary Heaps
A binary heap is a binary tree that keeps a partial order: each node has a value less than its parent and larger than either of its two children; there is no specific order imposed between siblings. (You may also do it the other way around: you can design heaps in which any node has a value larger than its parent, you basically only need to reverse the comparison.)
Because there is no order between siblings, it is not possible to find a particular element without potentially searching the whole heap. Therefore, a heap is not very good if you need random access to specific nodes. But if you're interested in always finding the largest (or smallest) item, then a heap is a very efficient data structure.
Heaps are used for solving a number of computer science problems, and also serve as the basis for an efficient and very popular sorting technique called heap sort.
For a human, it is useful to represent a heap in a tree-like
form. But a computer can store a heap as a simple array (not
even a nested array). For this, the index of an element is
used to compute the index of its parent or its two children.
Roughly speaking, the children of an element are the two locations where the
indices are about double its index; conversely, the parent
of a node is located at about half its index. If the heap
starts at index 0, the exact formulas for a node with index
$n are commonly as follows:
- Parent:
int( ($n-1)/2 ) - Left child:
2*$n + 1 - Right child:
2*$n + 2
The root node is at index 0. Its children are at positions 1 and 2. The children of 1 are 3 and 4 and the children of 2 are 5 and 6. The children of 3 are 7 and 8, and so on.
Suppose we build a heap (in ascending order) from an array of all letters between a and v provided in any pseudo-random order, for example:
my @input = <m t f l s j p o b h v k n q g r i a d u e c>;
The resulting @heap might be something like this:
[a b g d c k j l f h e m n q p t r o i u s v]
We will see below on how to build such a heap from an unordered array, but let's concentrate for now on the heap properties.
The order in the @heap above may not be immediately obvious, but a is the smallest letter, and its two children, b and g, are larger than a.
The children of b are d and c and are larger than their parent b. Similarly, the children of g are k and j and are larger than
their parent. And so on. But it is rather inconvenient to manually check that we have a valid heap. So, we may want to write a helper subroutine
to display the heap in a slightly more graphical way:
sub print-heap (@heap) {
my $start = 0;
my $end = 0;
my $last = @heap.end;
my $step = 1;
loop {
say @heap[$start..$end];
last if $end == $last;
$start += $step;
$step *= 2;
$end += $step;
$end = $last if $end > $last;
}
}
This subroutine will not be used in the final code, but it proved to be very useful for debugging purposes.
If we pass the letter heap as an argument to this subroutine, it will be displayed in the following format:
(a)
(b g)
(d c k j)
(l f h e m n q p)
(t r o i u s v)
With a little bit of reformatting we can now see its structure in a tree-like format:
(a)
(b g)
(d c k j)
(l f h e m n q p)
(t r o i u s v ...)
And from that, we can now easily draw the tree:
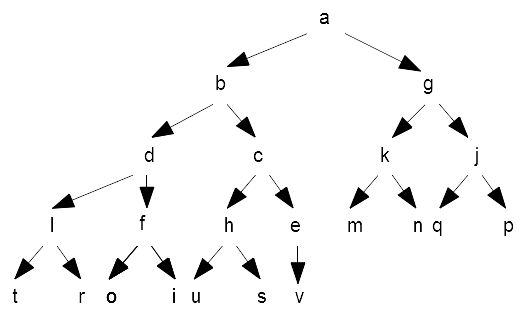
The important thing to notice is that there is no particular order between siblings, but children are always larger than their parent.
How to build a Binary Heaps
Since we'll be dealing later with integers (priorities) in descending order, we will abandon our ascending order letter heap. Let's suppose we have this heap example taken from the implementation section of the Wikipedia page on heaps):
my @heap = 100, 19, 36, 17, 12, 25, 5, 9, 15, 6, 11;
For the time being, we will consider it is a global variable accessible anywhere in the file.
Our print-heap helper subroutine would display it as:
(100)
(19 36)
(17 12 25 5)
(9 15 6 11)
We can see it's a valid heap (the children are always smaller than their parent).
Let's now add a new item, say 45, at the end of this array (for example with the push function). Of course, this item is not at its right place and the array is no longer a valid heap, but we can now use the following subroutine to move items around in order to obtain again a valid heap:
sub add-in-heap ($index is rw) {
my $index-val = @heap[$index];
while ($index) {
my $parent-idx = Int( ($index - 1) /2);
my $parent-val = @heap[$parent-idx];
last if $parent-val > $index-val;
@heap[$index] = $parent-val;
$index = $parent-idx;
}
@heap[$index] = $index-val;
}
The parameter passed is the index of the item that has just been added at the end of the array (11 in this example). This subroutine looks at the value of the parent of this new item. If the parent is larger than the new item, then we're done: the new array happens to be a valid heap (which is not the case in our example). If not, then we move the parent value to the position where we've just added the new element. Then we change the index of interest to the parent and iterate this way until either the elements are in the right place (the parent value is larger than the current index value) or the index become 0 (we've reached the root node). At this point, the loop ends and we can put the value we've added in the right place. If you think about it in terms of the binary tree shown above, we're really exploring the single path from the added element to the root (although we may not have to go all the way up to the root), the rest of the heap remains untouched.
Note that this subroutine is not designed to do anything special when fed with duplicate values. Here, duplicates will he handled gracefully and returned in the correct order. So, that's OK, it works fine, but we'll have to do something special about it when we will implement priority queues (if we had two priorities with the same value in the heap, we would be unable to predict the order in which items having the same priority will be pulled).
This subroutine will move around items from parent to child from the end to the beginning of the array (or at least until the new added value finds its right place), so that we get a new valid heap:
[100 19 45 17 12 36 5 9 15 6 11 25]
Using the helper subroutine to display the new heap outputs this:
(100)
(19 45)
(17 12 36 5)
(9 15 6 11 25)
I'll leave it to you to draw the tree to check that it is a proper heap.
We now know how to add an item to a existing heap, we can of course use that subroutine to add an item to an empty heap, and we can use that subroutine repeatedly to place each item in its proper place in order to create a heap from an input list in any order:
for @array.keys -> $i {
my $idx = $i;
add-in-heap $idx;
}
At the end of this loop, the @array will have been turned into a heap.
Removing One Element from the Heap
If we're looking for the largest element, it will be the root of the tree, i.e. the first item of the array.
Now, if we want to use this data structure to manage a priority queue, we will need at some point to delete the value in the root node and to reorganize the array so that it becomes again a legitimate heap. When we remove (100) from the above array, we have to choose the largest item between the two children, i.e. 45 in our example, and promote it as a new root node. And we can then propagate similarly the needed changes until the end of the array.
But the thermometer outside my house now shows 43.6 °C (in the shade), and it is more than 37°C inside. So, I'll be a bit lazy for a moment and, rather than writing such a new subroutine (which should be done if you want to be efficient and will be done below), I'll consider the array with the root node removed as an array in no particular order and use the code already written (the add-in-heap subroutine) to build a new heap from it:
sub take-from-heap {
my $result = shift @heap;
for @heap.keys -> $i {
my $idx = $i;
add-in-heap $idx;
}
return $result;
}
If we run that subroutine on our existing heap, it will return the largest item (the root node, i.e. 100) to the caller and reorganize the rest of the array into a new heap:
[45 36 17 15 25 5 9 12 6 11 19]
(45)
(36 17)
(15 25 5 9)
(12 6 11 19)
OK, this works, but reconstructing the full heap each time we remove an item is somewhat inefficient, which goes against the very purpose of heaps. What should a proper take-from-heap subroutine do? Take a look again at the binary tree displayed above. If we take off the root node value (a), we should replace it by b which is larger than g. It should be clear that we won't need to change anything in the g sub-tree. And we can recursively replace b by c, and then c by e and finally e by v. Nothing else needs to be changed. So basically we have to move up one step each of the nodes on the path of the smallest nodes in the b sub-tree. And, by the way, it is thanks to the fact that, whether we add a new item or remove an item from the heap, we only need to traverse one single path through the heap that insertion and deletion operations have a 0(log n) complexity and are therefore fairly fast. Implementing the ideas just described is not too difficult, but, for each visited node, we need to take into account three possible cases: this node may have 0, 1 or 2 children.
sub take-from-heap {
my $result = @heap[0];
my $index = 0;
loop {
my $left-index = 2 * $index + 1;
# right-index is $left-index + 1
unless (defined @heap[$left-index] or
defined @heap[$left-index + 1]) {
@heap.splice($index, 1);
last;
}
unless defined @heap[$left-index + 1] {
@heap[$index] = @heap[$left-index]:delete;
last;
}
unless defined @heap[$left-index] { # probably not happening
@heap[$index] = @heap[$left-index + 1]:delete;
last;
}
# both children are defined if we get here
my $next-index = ($left-index,
$left-index + 1).max({@heap[$_]});
@heap[$index] = @heap[$next-index];
$index = $next-index;
}
return $result;
}
If we run this new subroutine on our previous heap, we obtain this new heap:
[45 19 36 17 12 25 5 9 15 6 11]
(45)
(19 36)
(17 12 25 5)
(9 15 6 11)
Note that this is not the same heap as the one obtained before (same data but not in the same order), but this is another valid heap for such data. Using this subroutine repeatedly, we'll get the nodes in the same order: 45, 36, 25, 19, 17 etc. For example, let's run the new take-from-heap 10 times on our original heap and print out each time the removed first item and the resulting heap:
say "First item = ", take-from-heap, "; Heap: ", @heap for 1..10;
We can see that we have a valid heap at each iteration and pull the values in the right order:
First item = 100; Heap: [45 19 36 17 12 25 5 9 15 6 11]
First item = 45; Heap: [36 19 25 17 12 5 9 15 6 11]
First item = 36; Heap: [25 19 9 17 12 5 15 6 11]
First item = 25; Heap: [19 17 9 11 12 5 15 6]
First item = 19; Heap: [17 12 9 11 5 15 6]
First item = 17; Heap: [12 11 9 5 15 6]
First item = 12; Heap: [11 15 9 5 6]
First item = 11; Heap: [15 6 9 5]
First item = 15; Heap: [9 6 5]
First item = 9; Heap: [6 5]
So, it seems that we have a working algorithm to manage heaps. Let's turn now to priority queues.
A Priority Queue as a Heap
Basically, we want to manage our priorities with a heap, and each priority will be associated with an array containing the individual items in the order in which they were inserted. To give you immediately an idea of the data structure, the queue will look like this at a certain point during the execution of the tests in the script below:
[[10 [10 20]] [5 [5 15]] [2 [2 4 8 14 16]] [1 [1 7 11 13 17 19]] [3 [3 6 9 12 18]]]
The first item in the queue displayed above, [10 [10 20]], is the data structure for priority 10, which contains two elements, 10 and 20. The next one is for priority 5. And so on.
When we are inserting elements (item and priority), we first call insert_with_prio to check whether there is already an array for the given priority. If it already exists, we just add the item to the array of elements associated with this priority. If there no array with such priority, then we call add-to-queue to add a priority data structure into the heap (and reorganize the heap as we've done before). Similarly, when we call pull_highest_prio, we just pick up and return the first element from the data array of the first priority item. In the event that the data array of a given priority becomes empty, then we call take-from-heap to remove the priority data structure from the heap (and reorganize the heap as we've done before).
use v6;
sub new-queue {
my @queue; # an AoA
sub is_empty {
@queue.elems == 0;
}
sub insert_with_prio ($item, Int $prio) {
my $index = first {@queue[$_][0] == $prio}, @queue.keys;
if (defined $index) {
push @queue[$index][1], $item;
} else {
push @queue, [$prio, [$item]];
my $idx = @queue.end;
add-to-queue($idx);
}
}
sub pull_highest_prio {
return Nil if is-empty;
my $result = shift @queue[0][1];
take-from-heap if @queue[0][1].elems == 0;
return $result;
}
sub add-to-queue ($index is rw) {
my $index-val = @queue[$index];
while ($index) {
my $parent-idx = Int( ($index - 1) /2);
my $parent-val = @queue[$parent-idx];
last if $parent-val[0] > $index-val[0];
@queue[$index] = $parent-val;
$index = $parent-idx;
}
@queue[$index] = $index-val;
}
sub take-from-heap {
my $index = 0;
loop {
my $left-index = 2 * $index + 1;
# right-index is $left-index + 1
unless (defined @queue[$left-index] or
defined @queue[$left-index + 1]) {
@queue.splice($index, 1);
last;
}
unless defined @queue[$left-index + 1] {
@queue[$index] = @queue[$left-index]:delete;
last;
}
unless defined @queue[$left-index] {
@queue[$index] = @queue[$left-index + 1]:delete;
last;
}
# both children are defined if we get here
my $next-index = ($left-index,
$left-index + 1).max({@queue[$_][0]});
@queue[$index] = @queue[$next-index];
$index = $next-index;
}
}
return &is_empty, &insert_with_prio, &pull_highest_prio;
}
my (&is-empty, &insert, &pull-prio) = new-queue;
# Testing the above code: 20 insertions and then trying 30 deletions
for 1..20 -> $num {
insert($num,
$num %% 10 ?? 10 !!
$num %% 5 ?? 5 !!
$num %% 3 ?? 3 !!
$num %% 2 ?? 2 !!
1);
}
for 1..30 -> $num {
last if is-empty;
say pull-prio;
}
say "Empty queue" if is-empty();
This program displays more or less the same as before:
$ perl6 heap_queue.p6
10
20
5
15
3
6
9
12
18
2
4
8
14
16
1
7
11
13
17
19
Empty queue
Adding some additional print statements shows how the priority queue is evolving when we pull elements from it:
[[10 [10 20]] [5 [5 15]] [2 [2 4 8 14 16]] [1 [1 7 11 13 17 19]] [3 [3 6 9 12 18]]]
[ ... lines omitted for brevity ...]
Pulled 18; New queue: [[2 [2 4 8 14 16]] [1 [1 7 11 13 17 19]]]
Pulled 2; New queue: [[2 [4 8 14 16]] [1 [1 7 11 13 17 19]]]
Pulled 4; New queue: [[2 [8 14 16]] [1 [1 7 11 13 17 19]]]
Pulled 8; New queue: [[2 [14 16]] [1 [1 7 11 13 17 19]]]
Pulled 14; New queue: [[2 [16]] [1 [1 7 11 13 17 19]]]
Pulled 16; New queue: [[1 [1 7 11 13 17 19]]]
Pulled 1; New queue: [[1 [7 11 13 17 19]]]
Pulled 7; New queue: [[1 [11 13 17 19]]]
Pulled 11; New queue: [[1 [13 17 19]]]
Pulled 13; New queue: [[1 [17 19]]]
Pulled 17; New queue: [[1 [19]]]
Pulled 19; New queue: []
Empty queue
The code is quite long and is certainly not worth the effort if we're going to manage only 20 data elements and 5 priorities, as in our test cases above. But with much larger datasets and wider ranges of priority, it should be more efficient than our other implementations. If we're going to use many priority queues, the code of the add-to-queue and take-from-heap subroutines could be stored separately in a module, making the new-queue code much smaller and more manageable.
Note that the insert_with_prio subroutine is traversing sequentially the heap to figure out wether the priority data struture already exists in the heap. Depending on the number of priorities, this might become time consuming. It would be easy to add and maintain a hash keeping track of the existing priorities and their position in the heap, to avoid sequential search. I did not do it because I considered this to be an implementation detail that may be or may not be useful depending on the exact circumstances. I would probably do it if I were to write a heap priority library for a CPAN module.
A Heap Priority Queue in Perl 5
Asides from the small syntax differences between the two languages, there is nothing in what we did above in Perl 6 that cannot be done almost identically in Perl 5. For the benefit of readers who might not know yet the Perl 6 syntax or may otherwise find it easier to test and play in Perl 5, we provide here a translation of the heap priority queue in Perl 5:
#!/usr/bin/perl
use strict;
use warnings;
use feature qw/say/;
use Data::Dumper;
sub new_queue {
my @queue; # an AoA
my $add_to_queue = sub {
my $index = shift;
my $index_val = $queue[$index];
while ($index) {
my $parent_idx = int( ($index - 1) /2);
my $parent_val = $queue[$parent_idx];
last if $parent_val->[0] > $index_val->[0];
$queue[$index] = $parent_val;
$index = $parent_idx;
}
@queue[$index] = $index_val;
};
my $take_from_heap = sub {
my $index = 0;
while (1) {
my $left_index = 2 * $index + 1;
# right_index is $left_index + 1
unless (defined $queue[$left_index] or
defined $queue[$left_index + 1]) {
splice @queue, $index, 1;
last;
}
unless (defined $queue[$left_index + 1]) {
$queue[$index] = delete $queue[$left_index];
last;
}
unless (defined $queue[$left_index]) {
$queue[$index] = delete $queue[$left_index + 1];
last;
}
# both children are defined if we get here
my $next_index = $queue[$left_index][0]
> $queue[$left_index + 1][0] ?
$left_index : $left_index + 1;
$queue[$index] = $queue[$next_index];
$index = $next_index;
}
};
my $is_empty = sub {
scalar @queue == 0;
};
my $insert_with_prio = sub {
my ($item, $prio) = @_;
my $index;
for my $priority (0..$#queue) {
if($queue[$priority][0] == $prio) {
$index = $priority;
last;
}
}
if (defined $index) {
push @{$queue[$index][1]}, $item;
} else {
push @queue, [$prio, [$item]];
my $idx = $#queue;
$add_to_queue->($idx);
}
};
my $pull_highest_prio = sub {
return undef if $is_empty->();
my $result = shift @{$queue[0][1]};
$take_from_heap->() if scalar @{$queue[0][1]} == 0;
return $result;
};
return $is_empty, $insert_with_prio, $pull_highest_prio;
}
my ($is_empty, $insert, $pull_prio) = new_queue;
# Testing the above code: 20 insertions and deletions
for my $num (1..20) {
$insert->($num,
$num % 10 == 0 ? 10 :
$num % 5 == 0 ? 5 :
$num % 3 == 0 ? 3 :
$num % 2 == 0 ? 2 :
1);
}
for my $num (1..30) {
last if $is_empty->();
say $pull_prio->();
}
say "Empty queue" if $is_empty->();
I won't repeat the output displayed on the screen when running this program, as it is exactly the same as what we had with the Perl 6 implementation. And I won't comment further on it: almost everything I said before about the P6 implementation holds with this P5 version, so please refer to the above explanations on the P6 version if you need.
Note however the John Macdonald (one of the authors of the book Mastering Algorithms with Perl published by O'Reilly) wrote a collection of heap modules available on the CPAN. You might want to try some of them, especially his implementation of binary heaps.
Wrapping up
The next week Perl Weekly Challenge is due to start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on Sunday, August 4. And, please, also spread the word about the Perl Weekly Challenge if you can.
And see you hopefully at the European Perl Conference in Riga, Aug. 7 to 9, 2019.
 I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.
I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.
Leave a comment