laurent_r

These are some answers to the Week 26 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in several days from now (September 22, 2019). This blog post offers some solutions to this challenge. Please don't read on if you intend to complete the challenge on your own, which you're strongly encouraged to do.

Challenge # 1: Common Letters Count

Create a script that accepts two strings, let us call it, “stones” and “jewels”. It should print the count of “alphabet” from the string “stones” found in the string “jewels”. For example, if your stones is “chancellor” and “jewels” is “chocolate”, then the script should print “8”. To keep it simple, only A-Z,a-z characters are acceptable. Also make the comparison case sensitive.

We're given two strings and need to find out how many characters of the second string can be found in the first string.

Common Letters Count in Perl 5

This is straight forward. Our script should be given two arguments (else we abort the program). We split the first string into individual letters and store them in the %letters hash. Note that we filter out any character not in the [A-Za-z] character class. Then we split the second string into individual letters, keep only letters found in the %letters hash and finally coerce the resulting list of letters in a scalar context to transform it in a letter count (note that the scalar keyword isn't really needed here, as we have a scalar context anyway, but I included it to make it easier to understand).

#!/usr/bin/perl
use strict;
use warnings;
use feature qw/say/;

@ARGV == 2 or die "This script needs two strings are parameters";
my ($str1, $str2) = @ARGV;
my %letters = map {$_ => 1} grep /[A-Za-z]/, split "", $str1;
my $count = scalar grep { exists $letters{$_}} split "", $str2;
say "$str2 has $count letters from $str1";

Running the program:

$ perl count_letters.pl chocolate chancellor
chancellor has 8 letters from chocolate

$ perl count_letters.pl chancellor chocolate
chocolate has 8 letters from chancellor

$ perl count_letters.pl chancellor CHOCOLATE
CHOCOLATE has 0 letters from chancellor

We get the expected result. The last test shows that the comparison is case-sensitive, as requested in the specification.

Common Letters Count in Perl 6

We will use more or less the same idea as in P5, except that we'll use a set instead of a hash for storing unique letters of the first string.

use v6;

sub MAIN (Str $str1, Str $str2) {
    my $letters = $str1.comb.grep( /<[A..Za..z]>/ ).Set;
    my $count = $str2.comb.grep( { $_ (elem) $letters} ).elems;
    say "$str2 has $count letters from $str1";
}

This works as expected:

$ perl6 count_letters.p6 chocolate chancellor
chancellor has 8 letters from chocolate

$ perl6 count_letters.p6 chocolate CHANCELLOR
CHANCELLOR has 0 letters from chocolate

Mean Angles

Create a script that prints mean angles of the given list of angles in degrees. Please read wiki page that explains the formula in details with an example.

In mathematics, a mean of circular quantities is a mean which is sometimes better-suited for quantities like angles, day times, and fractional parts of real numbers. This is necessary since most of the usual means may not be appropriate on circular quantities. For example, the arithmetic mean of 0° and 360° is 180°, which is misleading because for most purposes 360° is the same thing as 0°.

A common formula for the mean of a list of angles is:

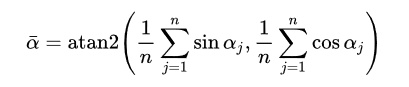
We just need to apply the formula, after having converted the input values from degrees to radians.

The Wikipedia page has the following example, that we will use in our tests: consider the following three angles as an example: 10, 20, and 30 degrees. Intuitively, calculating the mean would involve adding these three angles together and dividing by 3, in this case indeed resulting in a correct mean angle of 20 degrees. By rotating this system anticlockwise through 15 degrees the three angles become 355 degrees, 5 degrees and 15 degrees. The naive mean is now 125 degrees, which is the wrong answer, as it should be 5 degrees.

Mean Angles in Perl 5

There are a number of modules that could be used here to convert degrees to radians and radians to degrees, to compute arithmetic means and perhaps even to compute directly mean angles. But that wouldn't be a challenge if we were just using modules to dodge the real work.

So I wrote the deg2rad and rad2deg subroutines to do the angle unit conversions, and computed the arithmetic means of sines and cosines in a for loop.

As I do not have a use for such a program, I will implement the necessary subroutine and just use them in a series of tests.

#!/usr/bin/perl
use strict;
use warnings;
use feature qw/say/;
use constant PI => atan2(1, 0) * 2;
use Test::More;
plan tests => 9;


sub deg2rad { return $_[0] * PI /180; }
sub rad2deg { return $_[0] * 180 / PI }

sub mean {
    my @angles = map { deg2rad $_ } @_;
    my $count = @angles;
    my ($sum_sin, $sum_cos) = (0, 0);
    for my $angle (@angles) {
        $sum_sin += sin $angle;
        $sum_cos += cos $angle;
    }
    return rad2deg atan2 $sum_sin/$count, $sum_cos/$count;
}

is deg2rad(0), 0, "To rad: 0 degree";
is deg2rad(90), PI/2, "To rad: 90 degrees";
is deg2rad(180), PI, "To rad: 180 degrees";
is rad2deg(PI/2), 90, "To degrees: 90 degrees";
is rad2deg(PI), 180, "To degrees: 180 degrees";
is deg2rad(rad2deg(PI)), PI, "Roundtrip rad -> deg -> rad";
is rad2deg(deg2rad(90)), 90, "Roundtrip deg -> rad -> deg";
is mean(10, 20, 30), 20, "Mean of 10, 20, 30 degrees";
is mean(355, 5, 15), 5, "Mean of 355, 5, 15 degrees";

Running the tests displays the following:

$ perl angle-mean.pl
1..9
ok 1 - To rad: 0 degree
ok 2 - To rad: 90 degrees
ok 3 - To rad: 180 degrees
ok 4 - To degrees: 90 degrees
ok 5 - To degrees: 180 degrees
ok 6 - Roundtrip rad -> deg -> rad
ok 7 - Roundtrip deg -> rad -> deg
ok 8 - Mean of 10, 20, 30 degrees
ok 9 - Mean of 355, 5, 15 degrees

Update: As pointed out in a comment by Saif below, there is no need to divide both arguments of the atan2 built-in function: these arguments represent the abscissa and the ordinate of a point in the plan. Whether the two Cartesian coordinates are divided by count or not does not change the resulting polar angle calculated by atan2. Thus, we don't need to perform this division, and we don't even need the $count variable. The mean subroutine can be simplified as follows:

sub mean {
    my @angles = map { deg2rad $_ } @_;
    my ($sum_sin, $sum_cos) = (0, 0);
    for my $angle (@angles) {
        $sum_sin += sin $angle;
        $sum_cos += cos $angle;
    }
    return rad2deg atan2 $sum_sin, $sum_cos;
}

The tests display the same results as before.

End update.

Mean Angles in Perl 6

We will use essentially the same idea as in P5.

use v6;
use Test;

sub deg2rad (Numeric $deg) { return $deg * pi /180; }
sub rad2deg (Numeric $rad) { return $rad * 180 / pi }

sub mean (*@degrees) {
    my @radians = map { deg2rad $_ }, @degrees;
    my $count = @radians.elems;
    my $avg-sin = ([+] @radians.map( {sin $_})) / $count; 
    my $avg-cos = ([+] @radians.map( {cos $_})) / $count; 
    return rad2deg atan2 $avg-sin, $avg-cos;
}
plan 9;
is deg2rad(0), 0, "To rad: 0 degree";
is deg2rad(90), pi/2, "To rad: 90 degrees";
is deg2rad(180), pi, "To rad: 180 degrees";
is rad2deg(pi/2), 90, "To degrees: 90 degrees";
is rad2deg(pi), 180, "To degrees: 180 degrees";
is deg2rad(rad2deg(pi)), pi, "Roundtrip rad -> deg -> rad";
is rad2deg(deg2rad(90)), 90, "Roundtrip deg -> rad -> deg";
is-approx mean(10, 20, 30), 20, "Mean of 10, 20, 30 degrees";
is-approx mean(355, 5, 15), 5, "Mean of 355, 5, 15 degrees";

And this is the output produced when running the script:

perl6  angle-mean.p6
1..9
ok 1 - To rad: 0 degree
ok 2 - To rad: 90 degrees
ok 3 - To rad: 180 degrees
ok 4 - To degrees: 90 degrees
ok 5 - To degrees: 180 degrees
ok 6 - Roundtrip rad -> deg -> rad
ok 7 - Roundtrip deg -> rad -> deg
ok 8 - Mean of 10, 20, 30 degrees
ok 9 - Mean of 355, 5, 15 degrees

Note that I had to use the is-approx function of the Test module (instead of the simple is function) for tests computing the mean because I would otherwise get failed tests due to rounding issues:

# Failed test 'Mean of 10, 20, 30 degrees'
# at angle-mean.p6 line 22
# expected: '20'
#      got: '19.999999999999996'
not ok 9 - Mean of 355, 5, 15 degrees

As you can see, the program computes 19.999999999999996, where I expect 20, which is nearly the same numeric value.

I actually expected similar problems with Perl 5, but, for some reason, it did not occur. Perhaps the P5 Test::More module has a built-in approximate numeric comparison that silently takes care of such problems.

Update: as note above in the P5 section of this task following Saif's comment, we don't really need to divide the arguments of the atan2 built-in function by the number of angles. The mean subroutine can be simplified as follows:

sub mean (*@degrees) {
    my @radians = map { deg2rad $_ }, @degrees;
    my $sum-sin = [+] @radians.map( {sin $_}); 
    my $sum-cos = [+] @radians.map( {cos $_}); 
    return rad2deg atan2 $sum-sin, $sum-cos;
}

The tests display the same results as before.

End update.

Wrapping up

The next week Perl Weekly Challenge is due to start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on Sunday, September, 29. And, please, also spread the word about the Perl Weekly Challenge if you can.