laurent_r

These are some answers to the Week 43 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a couple of days (January 19, 2020). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Challenge # 1: Olympic Rings

There are 5 rings in the Olympic Logo as shown below. They are color coded as in Blue, Black, Red, Yellow and Green.

We have allocated some numbers to these rings as below: Blue: 8 Yellow: 7 Green: 5 Red: 9

The Black ring is empty currently. You are given the numbers 1, 2, 3, 4 and 6. Write a script to place these numbers in the rings so that the sum of numbers in each ring is exactly 11.

If all five rings have a score of 11, then the total must be 55. The current total is 29, and the sum of the additional numbers is 16. So we cannot reach 55 by using each of the numbers only once, some will have to be used more than one time. So we don’t worry about using one of the additional numbers several times.

Olympic Rings in Perl

The idea of the solution is to take each ring, compute how much is missing, i.e. the difference between the target value (11) and the current value. If that difference if one of the additional numbers, then we simply use it. If not, that we just try to fit the additional numbers, in descending order. We know that we will always find a solution, since we can always add 1 as many times as required to get to the target.

#!/usr/bin/perl
use strict;
use warnings;
use feature qw/say/;
use constant TARGET => 11;
use constant NUMS => (6, 4, 3, 2, 1);

my %rings = (black => 0, blue => 8, yellow => 7, green => 5, red => 9);


for my $ring (keys %rings) {
    say "Task not possible for $ring" and next if $rings{$ring} >= TARGET;
    my @complement = find_values($ring);
    say "The $ring ring starts with \t $rings{$ring}  and gets:  @complement."
}

sub find_values {
    my $ring = shift;
    my %numbers = map {$_ => 1} NUMS;
    my $diff = TARGET - $rings{$ring};
    return ($diff) if exists $numbers{$diff}; # not needed, for performance
    my @added_vals;
    for my $num (NUMS) {
        while ($num <= $diff) {
            push @added_vals, $num;
            $diff -= $num;
            return @added_vals if $diff == 0;
        }       
    } 
}

Running the program displays the following output:

$ perl olympic.pl
The blue ring starts with        8  and gets:  3.
The green ring starts with       5  and gets:  6.
The yellow ring starts with      7  and gets:  4.
The red ring starts with         9  and gets:  2.
The black ring starts with       0  and gets:  6 4 1.

Olympic Rings in Perl, Task Revisited

After I had completed the task in Perl, written the above, and while I was completing the tests on the same task in Raku, I suddenly noticed that the figure illustrating the Olympic rings had changed, probably at some time on Wednesday, January 15. And the new drawing of the rings is now as follows:

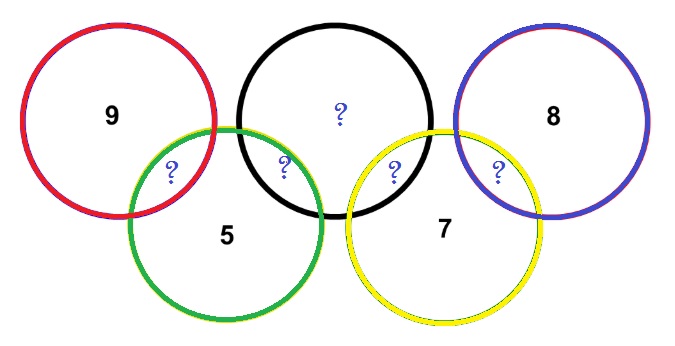
Looking at the drawing, we can now see that the task is asking us to insert the additional numbers in the ring intersections, which is something totally different.

Dear Mohammad, when you change the task after it has been posted, please send an e-mail to inform all the regular challengers. I’m pretty sure I’m not the only one to keep the challenge page loaded on a tab for several days without updating it.

The slight difficulty here is to model the geometry of the rings into some Perl data structure. Looking at the rings, it seems obvious we need to complete the red and blue rings to be able to complete unambiguously the green and yellow rings (respectively). And, once we have the green and yellow rings, we can finally complete the black one. I decided to make it as simple as possible and to use the @ring_sequences array of arrays (AoA) to store this information (and dealing with the black ring at the end).

use strict;
use warnings;
use feature qw /say/;
use constant TARGET => 11;                      

my %nums = map { $_ => 1 } qw/1 2 3 4 6/;
my %rings = (
    blue   => 8,
    yellow => 7,
    green  => 5,
    red    => 9,
    black  => 0
);

my @ring_sequences = ( [qw <red green>], [qw <blue yellow>] );
my @black_vals;

for my $seq_ref (@ring_sequences) {
    my $diff = 0;
    for my $ring (@$seq_ref) {
        $rings{$ring} += $diff;
        say "Added $diff to $ring ring, " if $diff;
        $diff = TARGET - $rings{$ring};
        die "No way" unless exists $nums{$diff};
        say "Added $diff to $ring ring";
        $rings{$ring} += $diff;
    }
    $rings{black} += $diff;
    push @black_vals, $diff;
}
my $black_diff = TARGET - $rings{black};
die "No way" unless exists $nums{$black_diff};
push @black_vals, $black_diff;
$rings{black} += $black_diff;
say "Added @black_vals to black ring";
say "\nFinal ring values:";
say "$_\t$rings{$_}" for keys %rings;

This is the output generated by this program:

$ perl olympic2.pl
Added 2 to red ring
Added 2 to green ring,
Added 4 to green ring
Added 3 to blue ring
Added 3 to yellow ring,
Added 1 to yellow ring
Added 4 1 6 to black ring

Final ring values:
blue    11
yellow  11
red     11
black   11
green   11

Olympic Rings (Revisited) in Raku

I did not find any way to use specific Raku features to do it other than just porting the Perl program (except for minor changes, such as using a Set instead of a hash). So, this is essentially the same ported to Raku:

use v6;

constant target = 11;          
my $nums = Set.new(1, 2, 3, 4, 6);
my %rings = 
    blue   => 8,
    yellow => 7,
    green  => 5,
    red    => 9,
    black  => 0
;

my @ring-sequences = ["red", "green"], ["blue", "yellow"];
my @black-vals;

for @ring-sequences -> @seq {
    my $diff = 0;
    for @seq -> $ring {
        %rings{$ring} += $diff;
        say "Added $diff to $ring ring" if $diff;
        $diff = target - %rings{$ring};
    die "No way" unless $nums{$diff};
        say "Added $diff to $ring ring";
        %rings{$ring} += $diff;
    }
    %rings{'black'} += $diff;
    push @black-vals, $diff;
}
my $black_diff = target - %rings{'black'};
die "No way" unless $nums{$black_diff}:exists;
push @black-vals, $black_diff;
%rings{'black'} += $black_diff;
say "Added @black-vals[] to black ring";
say "\nFinal ring values:";
say "$_\t%rings{$_}" for keys %rings;

And it produces essentially the same output:

$ perl6 olympic.p6
Added 2 to red ring
Added 2 to green ring
Added 4 to green ring
Added 3 to blue ring
Added 3 to yellow ring
Added 1 to yellow ring
Added 4 1 6 to black ring

Final ring values:
red     11
green   11
yellow  11
blue    11
black   11

Self-Descriptive Numbers

(Contributed by Laurent Rosenfeld.)

Write a script to generate self-descriptive Numbers in a given base.

In mathematics, a self-descriptive number is an integer m that in a given base b is b digits long in which each digit d at position n (the most significant digit being at position 0 and the least significant at position b - 1) counts how many instances of digit n are in m.

For example, if the given base is 10, then script should print 6210001000. For more information, please checkout wiki page.

First, to clarify my original intention: yes, this task is derived from a mail I sent Mohammad on Jan. 1, 2020, in which, besides wishing him and his family an happy new year, I also suggested a challenge on autobiographical numbers, the reason being that this new year, 2020, happens to be an autobiographical number (the first 2 says that there are two 0, the next 0 says that there is zero 1, and next 2 says that there are twp 2, and the final 0 says that there is no 3). Note that 2020 is also a self-descriptive number, but only in base 4, not in base 10 (because self-descriptive numbers must have a number of digits equal to the base). Now, since Wikipedia covers autobiographical numbers as a part of the Wikipedia entry on self-descriptive numbers, it seems that Mohammad thought I suggested a challenge on self-descriptive numbers, which is not exactly what I meant. Finding self-descriptive numbers in base 10 is quite challenging, because we’re supposed to review all numbers between 10 billion (1e10) and 100 billion - 1 (1e11 - 1), which is bound to take many hours. It can be done, but it’s expensive. However, we’ll see that there are faster solutions.

Self-Descriptive Numbers in Perl

Let’s start with a solution implementing directly the definition of self-descriptive numbers: in a given base b, we’re looking for a number that has b digits and in which each digit is equal the number of identical digits in the base-b representation of that number. We’ve seen the example of 2020 in base 4. There is another number matching this requirement in base 4: 1210 (equivalent to 100 in base 10). 1210 is 4 digit-long, and the 1 says that there is one 0, the 2 that there are two 1, the 1 that there is 1 2, and the 0 that there is no 3.

Note that it is known that there is no self-descriptive number for bases 2, 3, and 6.

If we are looking for self-descriptive numbers in base 4, we want to scan every number between 1000 (base 4) and 3333 (base 4), i.e. between 4 ** 3and 4 ** 4 -1. In decimal notation, this means each number between 64 and 255.

Then, for each number in this range, we check if it is self-descriptive.

We can start by implementing these rules as follows:

use strict;
use warnings;
use feature qw /say/;
use constant DIGITS => ('0'..'9', 'A'..'Z');

sub to_base_b {
    my($dec, $base) = @_;
    my @digits;
    while ($dec) {
        unshift @digits, (DIGITS)[$dec % $base];
        $dec = int($dec/$base);
    }
    return join "", @digits;
}
sub check_all_cases {
    my $base = shift;;
    for my $num ($base ** ($base -1) .. $base ** $base -1) {
        my $num_in_b = to_base_b ($num, $base);
        my @digits = split //, $num_in_b;
        my $success = 1;
        for my $rank (0..$base - 1) {
            my $nb_digits = $digits[$rank];
            my $num_occ = $num_in_b =~ s/$rank/$rank/g;
            if ($num_occ != $nb_digits) {
                $success = 0;
                last;
            }
        }
        say "Number in base $base: $num_in_b; decimal: $num" 
            if $success;
    }
}
my $base = shift;
check_all_cases($base);

Now, if we run this program for values 2 to 7, we get the following results:

$ perl self_descriptive.pl 2

$ perl self_descriptive.pl 3

$ perl self_descriptive.pl 4
Number in base 4: 1210; decimal: 100
Number in base 4: 2020; decimal: 136

$ perl self_descriptive.pl 5
Number in base 5: 21200; decimal: 1425   

$ perl self_descriptive.pl 6

$ perl self_descriptive.pl 7
Number in base 7: 3211000; decimal: 389305

The results are correct, but this is quickly getting slow (5.4 seconds for base 7 on my computer). It will be difficult to get to base 10, and impossible to get much further.

We can try some performance optimization. The Wikipedia article states that a self-descriptive number in base b must be a multiple of that base (or equivalently, that the last digit of the self-descriptive number must be 0). So we can skip the check for any number whose representation in a given base doesn’t end with 0. Also, all self-descriptive numbers have digit sums equal to their base. We can filter out those that don’t match these two conditions.

Adding these two criteria leads to the following modified check_all_cases subroutine:

sub check_all_cases {
    my $base = shift;;
    for my $num ($base ** ($base -1) .. $base ** $base -1) {
        my $num_in_b = to_base_b ($num, $base);
        next unless $num_in_b =~ /0$/;
        my @digits = split //, $num_in_b;
        my $sum = 0;
        $sum += $_ for split //, $num_in_b;
        next if $sum != $base;
        my $success = 1;
        for my $rank (0..$base - 1) {
            my $nb_digits = $digits[$rank];
            my $num_occ = $num_in_b =~ s/$rank/$rank/g;
            if ($num_occ != $nb_digits) {
                $success = 0;
                last;
            }
        }
        say "Number in base $base: $num_in_b; decimal: $num" 
            if $success;
    }
}

This helps a bit to improve performance (3.3 seconds instead of 5.4 for base 7), but not enough for larger bases.

The Wikipedia page referred to above states that, in base 7 and above, there is, if nothing else, a self-descriptive number of the form:

We can simply implement this formula for bases 7 and above. Our new program implements this for bases within the range 0 to 10:

use strict;
use warnings;
use feature qw /say/;
use constant DIGITS => ('0'..'9', 'A'..'Z');

sub find_self_descriptive {
    my $b = shift;
    return "No self-descriptive number for base $b" 
        if $b < 4 or $b == 6;
    if ($b == 4 or $b == 5) {
        return check_all_cases ($b);
    }
    my $dec_num = ($b - 4) * $b ** ($b - 1) 
        + 2 * $b ** ($b - 2) + $b ** ($b - 3) + $b ** 3;
    my $base_num = to_base_b ($dec_num, $b);
    return "Number in base $b: $base_num; decimal: $dec_num";
}

sub to_base_b {
    my ($dec, $base) = @_;
    my @digits;
    while ($dec) {
        unshift @digits, (DIGITS)[$dec % $base];
        $dec = int($dec/$base);
    }
    return join "", @digits;
}

sub check_all_cases {
    my $base = shift;;
    for my $num ($base ** ($base -1) .. $base ** $base -1) {
        my $num_in_b = to_base_b ($num, $base);
        next unless $num_in_b =~ /0$/;
        my @digits = split //, $num_in_b;
        my $sum = 0;
        $sum += $_ for split //, $num_in_b;
        next if $sum != $base;
        my $success = 1;
        for my $rank (0..$base - 1) {
            my $nb_digits = $digits[$rank];
            my $num_occ = $num_in_b =~ s/$rank/$rank/g;
            if ($num_occ != $nb_digits) {
                $success = 0;
                last;
            }
        }
        return "Number in base $base: $num_in_b; decimal: $num" if $success;
    }
}

say find_self_descriptive $_ for (1 .. 10);

This works fine and is very fast:

$ time perl self_descriptive.pl
No self-descriptive number for base 1
No self-descriptive number for base 2
No self-descriptive number for base 3
Number in base 4: 1210; decimal: 100
Number in base 5: 21200; decimal: 1425
No self-descriptive number for base 6
Number in base 7: 3211000; decimal: 389305
Number in base 8: 42101000; decimal: 8946176
Number in base 9: 521001000; decimal: 225331713
Number in base 10: 6210001000; decimal: 6210001000

real    0m0,061s
user    0m0,000s
sys     0m0,030s

Self-Descriptive Numbers in Raku

For solving this task in Raku, we’ll just port the last Perl version to Raku. Note that we no longer need the to_base_b base conversion subroutine, since Raku provides a base method to convert a number to a string representation of it in a given base. Raku offers a couple of additional features making the code somewhat simpler:

use v6;

sub find-self-descriptive (Int $b) {
    return check-all-cases ($b) if $b < 7;
    my $dec-num = ($b - 4) * $b ** ($b - 1) + 2 * $b ** ($b - 2) + $b ** ($b - 3) + $b ** 3;
    my $base-num = $dec-num.base($b);
    return "Number in base $b: $base-num; decimal: $dec-num";
}

sub check-all-cases (Int $base) {
    for $base ** ($base -1) .. $base ** $base -1 -> $num {
        my $num-in-b = $num.base($base);
        next unless $num-in-b ~~ /0$/;
        my @digits = $num-in-b.comb;
        next if $base != [+] @digits;
        my $success = True;
        for 0..$base - 1 -> $rank {
            if (+ $num-in-b.indices($rank) != @digits[$rank]) {
                $success = False;
                last;
            }
        }
        return "Number in base $base: $num-in-b; decimal: $num" if $success;
    }
    return "No self-descriptive number for base $base";
}

say .&find-self-descriptive for 1 .. 10;

This program displays the following output:

$ ./perl6 self_descriptive.p6
No self-descriptive number for base 1
No self-descriptive number for base 2
No self-descriptive number for base 3
Number in base 4: 1210; decimal: 100
Number in base 5: 21200; decimal: 1425
No self-descriptive number for base 6
Number in base 7: 3211000; decimal: 389305
Number in base 8: 42101000; decimal: 8946176
Number in base 9: 521001000; decimal: 225331713
Number in base 10: 6210001000; decimal: 6210001000

Wrapping up

The next week Perl Weekly Challenge is due to start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on Sunday, January 26, 2020. And, please, also spread the word about the Perl Weekly Challenge if you can.