laurent_r

These are some answers to the Week 148 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on January 23, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Eban Numbers

Write a script to generate all Eban Numbers <= 100.

*An Eban number is a number that has no letter ‘e’ in it when the number is spelled in English (American or British).

Example:

2, 4, 6, 30, 32 are the first 5 Eban numbers.

The task asks us to list the Eban integers smaller than or equal to 100. To start with, 100 (“one hundred”) has two ‘e’, so it is not an Eban number. So we can limit our search to all Eban Numbers < 100, so that we can limit our search to integers with one or two digits.

For the single-digit integers and for the second digit of integers with two digits, we need to exclude: 1,3,5,7,8,and 9. For the first digit of two-digit integers (pronounced eleven, twelve, xxxxteen, twenty, thirty, etc. in English), wee need to exclude: 1x, 2x, 7x, 8x, 9x.

Eban Numbers in Raku

Implementing the exclusion rules detailed above is fairly easy with two regexes:

my @ebans = grep { ! /<[135789]>$/ and ! /<[12789]>\d/ }, 1..99;
say @ebans;

This script displays the following output:

$ raku ./eban.raku
[2 4 6 30 32 34 36 40 42 44 46 50 52 54 56 60 62 64 66]

This script is so simple that we can make it a Raku one-liner:

raku -e 'say grep { ! /<[135789]>$/ and ! /<[12789]>\d/ }, 1..99;'
(2 4 6 30 32 34 36 40 42 44 46 50 52 54 56 60 62 64 66)

Eban Numbers in Perl

We can implement the same exclusion rules in Perl:

use strict;
use warnings;
use feature "say";

my @ebans = grep { ! /[135789]$/ and ! /[12789]\d/ } 1..99;
say "@ebans";

This script displays the following output:

$ perl ./eban.pl
2 4 6 30 32 34 36 40 42 44 46 50 52 54 56 60 62 64 66

This can also be a Perl one-liner:

$ perl -E 'say join " ", grep { ! /[135789]$/ and ! /[12789]\d/ } 1..99;'
2 4 6 30 32 34 36 40 42 44 46 50 52 54 56 60 62 64 66

Task 2: Cardano Triplets

Write a script to generate first 5 Cardano Triplets.

A triplet of positive integers (a,b,c) is called a Cardano Triplet if it satisfies the below condition.

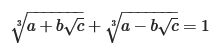
Example:

(2,1,5) is the first Cardano Triplets.

In order to be able to generate the 5 first Cardano triplets, we would need to clarify what first means. In other words, we would need to establish an order relation on the Cardano triplets. Such order could be any of many things: order the triplets in accordance with the first integer of the triplet (a), or the second (b), or the third (c). It could also be the sum of the 3 triplets. Or some weighted average. Whatever. I will simply list the 5 first triplets that I find, which is as valid an order as any other.

Cardano Triplets in Raku

We implement a subroutine, is-cardano-triplet, to find whether a triplet of integers satisfies the criteria for Cardano triplets. Here we encountered an unexpected difficulty: the exponentiation operator (**) returns “Not a number” (NaN) when the base is negative and the power a (non-integer) rational number:

say (-2) ** (1/3);    # NaN

I don’t understand why, as I believe that this is a perfectly valid mathematical operation. I would definitely understand such a result for the square root of a negative number, but I don’t for the cubic root. The scientific calculator on my mobile phone and Excel both return proper values with such input.

In order for the above equation to hold, the second term has to be negative, as the first term will always be a positive number larger than 1. So, the subroutine returns false if the second term is positive. Then we can compute the cubic root of the absolute value of the second term, and change the addition of the two terms with a subtraction. In addition, we need to use the =~= approximately-equal operator to compare floating point numbers with an integer as 1.

use v6;
constant MAX = 5;

sub is-cardano-triplet (\a, \b, \c) {
    return False if a - b * c.sqrt > 0;
    my $val = ((a + b * c.sqrt) ** (1/3)) - ((- a + b * c.sqrt) ** (1/3));
    return $val =~= 1
}

my @values = 1..100;
my $count = 0;
OUT: for @values -> $i {
    for @values -> $j {
        for @values -> $k {
            if is-cardano-triplet $i, $j, $k {
                say "$i $j $k";
                $count++;
                last OUT if $count >= MAX;
            }
        }
    }
}
say "Duration: ", now - INIT now;

This program displays the following output:

$ raku ./cardano.raku
2 1 5
5 1 52
5 2 13
8 3 21
11 4 29
Duration: 6.621876

We have here used the first 100 integers as input. If we use integers between 1 and 200, we find another triplet with 8 as the first integer: 8, 1, 189. But again, we have no special order, we just take the first triplets that we find.

Cardano Triplets in Perl

This is essentially a port to Perl of the Raku program above. Just like in Raku, the exponentiation operator (**) returns “Not a number” (NaN) when the base if negative and the power a (non-integer) rational number. So we use the same method to work around this limitation. Also, since Perl does not have an approximately-equal (=~=) operator, we implement it manually: we check that the absolute value of the difference between the equation result and 1 is less than a given very small value (set here to 0.000001).

use strict;
use warnings;
use feature "say";
use constant MAX => 5;

sub is_cardano_triplet {
    my ($a, $b, $c) = @_;
    return 0 if $a - $b * sqrt($c) > 0;
    my $val = (($a + $b * sqrt($c)) ** (1/3)) - ((- $a + $b * sqrt($c)) ** (1/3));
    # say $val;
    return abs($val - 1) < 0.000001;
}

my @values = 1..100;
my $count = 0;
OUT: for my $i (@values) {
    for my $j (@values) {
        for my $k (@values) {
            if (is_cardano_triplet $i, $j, $k) {
                say "$i $j $k";
                $count++;
                last OUT if $count >= MAX;
            }
        }
    }
}

This program displays the following output:

$ time perl cardano.pl
2 1 5
5 1 52
5 2 13
8 3 21
11 4 29

real    0m0,175s
user    0m0,108s
sys     0m0,046s

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on January 30, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.