laurent_r

These are some answers to the Week 153 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on February 27, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Left Factorials

Write a script to compute Left Factorials of 1 to 10. Please refer OEIS A003422 for more information.

Expected Output:

1, 2, 4, 10, 34, 154, 874, 5914, 46234, 409114

The task specification unfortunately lacks a precise definition of left factorials. Looking at OEIS A003422, I found we could use the following recursive definition:

a(0) = 0
a(1) = 1
a(n) = n*a(n - 1) - (n - 1)*a(n - 2)

After I did some of the implementations below, I found another definition making more sense of left factorials (a.k.a. factorial sums). Left factorial of the integer n is the sum of the factorials of the integers from 0 to n - 1. Left factorial is commonly denoted by a prefixed exclamation mark. So we have:

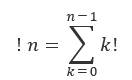
with ! 0 = 0.

Left Factorials in Raku

The implementation can easily be derived from the recursive definition above, except that I prefer an iterative implementation (well, it could probably be argued it is sort of a cached recursive approach, even though there is no recursive subroutine call):

my @a = 0, 1, 2;
for 3..10 -> $n {
    @a[$n] = $n * @a[$n -1] - ($n - 1) * @a[$n - 2];
}
say @a[1..10];

This program displays the following output:

$ raku ./left_fact.raku
(1 2 4 10 34 154 874 5914 46234 409114)

In Raku, we can also use sigilless variables) to make the code look more like a math formula:

my @a = 0, 1;
for 2..10 -> \n {
    @a[n] = n * @a[n -1] - (n - 1) * @a[n - 2];
}
say @a[1..10];

This new version displays the same output.

As mentioned before, the above implementations were done before I found about the second (summation of factorials) formula. Raku has reduction metaoperators) making it easy to implement factorials and summations. This can lead to this concise Raku one-liner using two triangular reduction operators:

$ raku -e 'say (|[\+] 1, (|[\*] 1..*))[0..9]'
(1 2 4 10 34 154 874 5914 46234 409114)

In addition, we could also define a prefix ! operator, but this has the drawback of redefining the standard negation prefix operator !. This does work, but it’s probably not very wise to do so.

Left Factorials in Perl

Again, the implementation can easily be derived from the recursive definition provided above:

use strict;
use warnings;
use feature "say";

my @a = (0, 1);
for my $n (2..10) {
    $a[$n] = $n * $a[$n -1] - ($n - 1) * $a[$n - 2];
}
say "@a[1..10]";

This program displays the following output:

$ perl ./left_fact.pl
1 2 4 10 34 154 874 5914 46234 409114

Left Factorials in Other Languages

In Julia

Using the recursive definition of left factorials:

a = [1, 2] # Julia arrays start with index 1

for n in 3:10
    push!(a, n * a[n - 1] - (n - 1) * a[n - 2])
end
println(a)

Output:

$ julia ./left_fact.jl
[1, 2, 4, 10, 34, 154, 874, 5914, 46234, 409114]

In Ring

Here, we use the summation of factorials definition. For each iteration in the for loop, we multiply fact by the loop variable to obtain the new factorial, and we add the new factorial to the sum variable. For some strange reason, see left_fact + " "' doesn’t output a space after the variable value, where as see " " + left_fact does what we want. To me, it looks like a small bug in the language, but I may be missing something.

left_fact = 1
fact = 1
for i = 1 to 10
    see " " + left_fact 
    fact *= i
    left_fact += fact  
next
see " " + nl

Output:

$ ring ./left_fact.ring
1 2 4 10 34 154 874 5914 46234 409114

In Python

Again using the summation of factorials definition.

fact = 1
left_fact = 1

for n in range (1, 11):
    print(left_fact)
    fact = fact * n
    left_fact = left_fact + fact

Output:

$ python3 ./left_fact.py
1
2
4
10
34
154
874
5914
46234
409114

Note that I didn’t remember how to how to output data without a new line in Python, and I was too lazy to spend time to find out. This is proverbially left as an exercise to the reader, as this output fits the specification bill.

In Awk

Using the summation of factorials definition.

BEGIN {
    left_fact = 1
    fact = 1
    for (i = 1; i <= 10; i++) {
        printf "%d ", left_fact
        fact *= i
        left_fact += fact  
    }
    printf "\n"
}

Output:

$ awk -f left_fact.awk
1 2 4 10 34 154 874 5914 46234 409114

In C

Using the summation of factorials definition.

#include <stdio.h>

int main () {
    int sum = 1;
    int fact = 1;
    for (int i = 1; i <= 10; i++) {
        printf("%d ", sum);
        fact *= i;
        sum += fact;
    }
    printf ("\n");
    return 0;
}

Output:

$ ./test-left
1 2 4 10 34 154 874 5914 46234 409114

In Bc

Using the summation of factorials definition.

sum = 1
fact = 1

for (n = 1; n <= 10; n ++) {
    print sum, " "
    fact = fact * n
    sum = sum + fact
}

Output:

$ bc left_fact.bc
bc 1.06.95
Copyright (...)
1 2 4 10 34 154 874 5914 46234 409114

In Tcl

Using the summation of factorials definition.

set left_fact 1
set fact 1
puts -nonewline $left_fact

for {set i 1} {$i <= 10} {incr i} {
    puts -nonewline "${left_fact} "
    set fact [expr $fact * $i]
    set left_fact [expr $left_fact + $fact]

}
puts ""

Output:

$ tclsh ./left_fact.tcl
11 2 4 10 34 154 874 5914 46234 409114

In R

Using the summation of factorials definition.

left_fact <- 1
fact <- 1

for (i in 1:10) {
    cat(left_fact, '')
    fact <- fact * i
    left_fact <- left_fact + fact
}
cat("\n")

Output:

$ Rscript left_fact.r
1 2 4 10 34 154 874 5914 46234 409114

In Pascal

Using the summation of factorials definition.

Program leftfact;

var
    fact, left_fact: longint;
    i: integer;

begin
    left_fact := 1;
    fact := 1;
    for i := 1 to 10 do begin
        write(left_fact, ' ');
        fact := fact * i;
        left_fact := left_fact + fact;
    end;
    writeln('');
end.

Output:

$ ./left_fact
1 2 4 10 34 154 874 5914 46234 409114

In Rust

Using the summation of factorials definition.

fn main() {
    let mut fact = 1;
    let mut left_fact = 1;
    for n in 1..11 {
        println!("{}", left_fact);
        fact = fact * n;
        left_fact = left_fact + fact;
    }
}

Output:

$ ./left_fact
1
2
4
10
34
154
874
5914
46234
409114

In Go

Using the summation of factorials definition.

package main

import "fmt"

func main() {
    left_fact := 1
    fact := 1
    for i := 1; i <= 10; i++ {
        fmt.Printf("%d ", left_fact)
        fact *= i
        left_fact += fact
    }
    fmt.Printf("\n")
}

Output:

1 2 4 10 34 154 874 5914 46234 409114

In Scala

Using the summation of factorials definition.

object fact_left extends App {
  var fact = 1
  var left_fact = 1
  for (n <- 1 to 10) {
    println(left_fact)
      fact *= n
    left_fact += fact
  }
}

Output: 1 2 4 10 34 154 874 5914 46234 409114

In Ruby

Using the summation of factorials definition.

fact = 1
left_fact = 1
for n in 1..10 
    printf "%d ", left_fact
    fact *= n
    left_fact += fact
end
printf "\n"

Output:

ruby left_fact.rb
1 2 4 10 34 154 874 5914 46234 409114

In Lua

Using the summation of factorials definition.

fact = 1
left_fact = 1
for n = 1, 10 do
    print(left_fact)
    fact = fact * n
    left_fact = left_fact + fact
end

Output:

$ lua left_fact.lua
1
2
4
10
34
154
874
5914
46234
409114

In Kotlin

Using the summation of factorials definition.

fun main() {
    var fact = 1
    var left_fact = 1
    for (i in 1..9) {
        fact *= i
        left_fact += fact
        print("$left_fact ")
    }
}

Output:

$ ./left_fact.kexe
2 4 10 34 154 874 5914 46234 409114

Task 2: Factorions

You are given an integer, $n.

Write a script to figure out if the given integer is factorion.

A factorion is a natural number that equals the sum of the factorials of its digits.

Example 1:

Input: $n = 145
Output: 1

    Since 1! + 4! + 5! => 1 + 24 + 120 = 145

Example 2:

Input: $n = 123
Output: 0

    Since 1! + 2! + 3! => 1 + 2 + 6 <> 123

We will slightly deviate from the task specification and write a subroutine that checks whether an integer is a factorion, and write a program to find all factorions in a given range.

Factorions in Raku

Here again, we use twice the reduction metaoperators), one ([*] 1..$_) to compute the factorial of a digit, and one ([+]) to sum up the digit factorials.

sub is_factorion (Int $in) {
    my $sum = [+] map { [*] 1..$_ }, $in.comb;
    return $sum == $in;
}
say $_ if is_factorion $_ for 1..50000;

We chose here an upper limit of 50,000 because it is known and proven that there are only 4 factorions in the decimal system, all smaller than 50,000. This solution is concise and elegant and the is_factorion subroutine could easily be boiled down to a single code line:

sub is_factorion (Int $in) {
    return $in == [+] map { [*] 1..$_ }, $in.comb;
}

This program displays the following output:

$ time raku ./factorion.raku
1
2
145
40585

real    0m13,079s
user    0m0,015s
sys     0m0,030s

Note that I timed the execution because I felt it was a bit slow. The reason for that slowness is that we’re computing the factorial of each digit a very large number of times. It is significantly more efficient to cache the factorials of each digit, for example by storing in an array (@fact) the precomputed factorials of digits 0 to 9.

my @fact = map { [*] 1..$_ }, 0..9;
sub is_factorion (Int $in) {
    my $sum = [+] map { @fact[$_] }, $in.comb;
    return $sum == $in;
}
say $_ if is_factorion $_ for 1..50000;

This modified program displays the following output and timings:

$ time raku ./factorion.raku
1
2
145
40585

real    0m1,553s
user    0m0,000s
sys     0m0,015s

So caching the digit factorials made the program about 8.5 times faster.

Factorions in Perl

In Perl, we implemented directly the cached version with a @digit_fact array:

use strict;
use warnings;
use feature "say";

sub fact {
    my $i = shift;
    my $prod = 1;
    $prod *= $_ for 2..$i;
    return $prod;
}

my @digit_fact = map {fact $_} 0..9;

sub is_factorion {
    my $in = shift;
    my $sum = 0;
    $sum += $_ for map { $digit_fact[$_] } split //, $in;
    return $sum == $in;
    #say $sum;
}
for (1..50000) {
    say $_ if is_factorion($_)
}

This program displays the following output:

$ time perl ./factorion.pl
1
2
145
40585

real    0m0,182s
user    0m0,140s
sys     0m0,015s

Factorions in Other Languages

In Julia

fact = map(x -> factorial(x), Vector(0:9))

function is_factorion(num)
    sum = 0
    start_num = num
    for n in 1:length(string(num))
        sum += fact[num % 10 + 1] # Julia arrays start at 1
        num = num ÷ 10
    end
    return sum == start_num
end

for i in 1:50000
    if is_factorion(i)
        println(i)
    end
end

Output:

$ julia ./factorion.jl
1
2
145
40585

In Ring

In Ring, list index starts at 1. That makes index management a bit complicated in this case, because we need to store the factorial of 0. So factorial 0 is stored at index 1, and all the others are shifted by 1. It’s not a problem, but it makes the code look a bit unnatural.

fact = [1, 1]
for k = 2 to 9
    add (fact, k * fact[k]) # list indices start at 1
next
# see fact + nl
for n = 1 to 50000
    if is_factorion(fact, n)
        see n + nl
    ok
next

func is_factorion fact, input
    sum = 0
    n = "" + input
    for i = 1 to len(n)
        digit = n[i]
        sum += fact[1 + digit]
    next
    return input = sum

Output:

$ ring ./factorion.ring
1
2
145
40585

In Python

fact = [1] * 10
for n in range (1, 10):
    fact[n] = n * fact[n - 1]

def is_factorion (input):
    sum = 0
    n = str(input)
    for i in range (0, len(n)):
        sum = sum + fact[int(n[i])]

    return input == sum

for n in range(1, 50000):
    if is_factorion(n):
        print(n)

Output:

$ python3 ./factorion.py
1
2
145
40585

In C

#include <stdio.h>

char is_factorion(int fact[], int num) {
    int sum = 0;
    int n = num;
    while (n > 0) {
        sum += fact[n % 10];
        n /= 10;
    }
    return num == sum;
}

int main() {
    int fact[10];
    fact[0] = 1;
    for (int i = 1; i <= 9; i++) {
        fact[i] = i * fact[i - 1];
    }

    for (int n = 1; n < 50000; n++) {
        if (is_factorion(fact, n)) {
            printf("%d ", n);
        }
    }
    printf("\n");
    return 0;
}

Output:

$ ./factorion 1 2 145 40585

In Awk

function populate_fact() {
    fact[0] = 1
    for (n = 1; n <= 9; n++) {
        fact[n] = n * fact[n - 1]
    }
}
function is_factorion(num) {
    sum = 0
    start_num = num
    for (n = 0; n < length(start_num); n++) {
        sum += fact[num % 10]
        num = int(num / 10)
    }
    return sum == start_num
 }
BEGIN {
    populate_fact()
    for (i = 1; i <= 50000; i++) {
        if (is_factorion(i)) {
            print i
        }
    }
}

Output:

$ awk -f factorion.awk
1
2
145
40585

In Bc

fact[0] = 1
for (n = 1; n <= 9; n++) {
    fact[n] = n * fact[n - 1]
}
for (n = 1; n <= 50000; n++) {
    sum = 0
    i = n
    while (i > 0) {
        sum += fact[i % 10]
        i /= 10
    }
    if (sum == n) {
        print n, " "
    }
}
halt

Output:

$ bc  factorion.bc
bc 1.06.95
Copyright (...)
1 2 145 40585

In Scala

object factorion extends App {
  def is_factorion(fact: Array[Int], num: Int): Boolean = {
    var sum = 0
    var i = num
    while (i > 0) {
      sum += fact(i % 10)
      i /= 10
    }
    return num == sum
  }

  val fact = new Array[Int](12)
  fact(0) = 1
  for (n <- 1 to 9) {
    fact(n) = n * fact(n - 1)
  }

  for (j <- 1 to 50000) {
    if (is_factorion(fact, j)) {
      println(j)
    }
  }
}

Output:

1
2
145
40585

In Lua

function is_factorion(fact, num)
    sum = 0
    i = num
    while i > 0 do
        sum = sum + fact[ 1 + i % 10]
        i = math.floor(i / 10)
    end
    return num == sum
end

fact = {1}
for n = 1, 10 do
    table.insert(fact, n * fact[n])
end
for j = 1, 50000 do
    if is_factorion(fact, j) then
        print(j)
    end
end

Output:

$ lua factorion.lua
1
2
145
40585

In Kotlin

fun main() {
    var fact = mutableListOf<Int>()
    fact.add(1)
    for (n in 1..9) {
        fact.add(n * fact[n-1])
    }
    for (num in 1..50000) {
        var i = num
        var sum = 0
        while (i > 0) {
            sum += fact[i % 10]
            i /= 10
        }
        if (num == sum) print ("$num ")
    }
}

Output:

$ ./factorion.kexe
1 2 145 40585

In Ruby

def is_factorion(fact, num)
    sum = 0
    i = num
    while i > 0
        i, d = i.divmod(10)
        sum += fact[d]
    end
    return num == sum
end

fact = [1]
for n in 1..10
    fact.push(n * fact[n - 1])
end
for j in 1..50000
    if is_factorion(fact, j)
        printf "%d ", j
    end
end
printf("\n")

Output:

$ ruby factorion.rb
1 2 145 40585

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on March 6, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.