laurent_r

These are some answers to the Week 157 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a couple of days from now (on March 27, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Pythagorean Numbers

You are given a set of integers.

Write a script to compute all three Pythagorean Means i.e Arithmetic Mean, Geometric Mean and Harmonic Mean of the given set of integers. Please refer to wikipedia page for more informations.

Example 1:

Input: @n = (1,3,5,6,9)
Output: AM = 4.8, GM = 3.9, HM = 2.8

Example 2:

Input: @n = (2,4,6,8,10)
Output: AM = 6.0, GM = 5.2, HM = 4.4

Example 3:

Input: @n = (1,2,3,4,5)
Output: AM = 3.0, GM = 2.6, HM = 2.2

Since the task description doesn’t explain it, let me provide some formulas for arithmetic mean (AM), geometric mean (GM) and harmonic mean (AM):

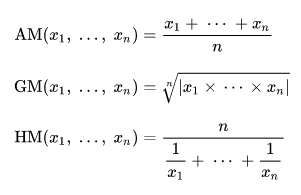
Pythagorean Numbers in Raku

The Raku build-in [ ] reduce metaoperator makes it possible to compute each of the means with just one simple code-line:

for (1,3,5,6,9), (2,4,6,8,10), (1,2,3,4,5) -> @in {
    my $n = @in.elems;
    my $am = ([+] @in)/ $n;
    my $gm = ([*] @in)** (1/$n);
    my $hm = $n / ([+] map { 1/$_}, @in);
    printf  "%-10s -> AM: %0.1f, GM: %0.1f, HM: %0.1f\n", "@in[]", $am, $gm, $hm;
}

This script displays the following output:

$ raku ./means.raku
1 3 5 6 9  -> AM: 4.8, GM: 3.8, HM: 2.8
2 4 6 8 10 -> AM: 6.0, GM: 5.2, HM: 4.4
1 2 3 4 5  -> AM: 3.0, GM: 2.6, HM: 2.2

Pythagorean Numbers in Perl

Perl doesn’t have a built-in reduce operator. We could either implement a reduce subroutine (I’ve done that in some previous PWC challenge), or compute each mean separately. Here, I’ve chosen the second option.

use strict;
use warnings;
use feature "say";

for my $test ([1,3,5,6,9], [2,4,6,8,10], [1,2,3,4,5]) {
    my @in = @$test;
    my $n = scalar @in;

    my $sum = 0;
    $sum += $_ for @in;
    my $am = $sum / $n;

    my $prod = 1;
    $prod *= $_ for @in;
    my $gm = $prod ** (1/$n);

    my $invsum = 0;
    $invsum += 1/$_ for @in;
    my $hm = $n / $invsum;
    printf  "%-10s -> AM: %0.1f, GM: %0.1f, HM: %0.1f\n", "@in", $am, $gm, $hm;
}

This script displays the following output:

$ perl ./means.pl 1 3 5 6 9 -> AM: 4.8, GM: 3.8, HM: 2.8 2 4 6 8 10 -> AM: 6.0, GM: 5.2, HM: 4.4 1 2 3 4 5 -> AM: 3.0, GM: 2.6, HM: 2.2

Task 2: Brazilian numbers

You are given a number $n > 3.

Write a script to find out if the given number is a Brazilian Number.

A positive integer number N has at least one natural number B where 1 < B < N-1 where the representation of N in base B has same digits.

Example 1:

Input: $n = 7
Output: 1

Since 7 in base 2 is 111.

Example 2:

Input: $n = 6
Output: 0

Since 6 in base 2 is 110,
      6 in base 3 is 20 and
      6 in base 4 is 12.

Example 3:

Input: $n = 8
Output: 1

Since 8 in base 3 is 22.

Well to start with, I find the above definition of a Brazilian number to be not completely clear. This is another definition:

Brazilian” numbers are numbers n such that there is a natural number b with 1 < b < n-1 such that the representation of n in base b has all equal digits.

First, the condition b < n-1 is important because every number n has representation 11 in base n-1. Then, every even number 2P >= 8 is Brazilian, because 2P = 2(P-1) + 2, which is 22 in base P-1 when P-1 > 2. Finally, we will extend the task to a search of all Brazilian numbers less than or equal to 36, since working with bases larger than 36 (the 1..9, 'a'..'z' range) would require a different data model.

Brazilian Numbers in Raku

We use the Raku built-in base to convert the input number to a string using $base as base.

sub is-brazilian (Int $n) {
    return True if $n %% 2 and $n >= 8;
    return False if $n <= 3;
    for 2..^($n-1) -> $base {
        return True if $n.base($base) ~~ /^(\d)$0+$/;
    }
    False;
}

say "Brazilian numbers less than or equal to 36 are:";
for 1..36 -> $m {
    print "$m " if is-brazilian $m;
}
say "";

This script displays the following Brazilian numbers:

$ raku ./brazilian_number.raku
Brazilian numbers less than or equal to 36 are:
7 8 10 12 13 14 15 16 18 20 21 22 24 26 27 28 30 31 32 33 34 35 36

Brazilian Numbers in Perl

The program below if basically a port to Perl of the Raku program above. The only significant change is that we had to implement the to_base_b subroutine to perform decimal-to-some_base conversion.

use strict;
use warnings;
use feature qw /say/;
use constant DIGITS => ('0'..'9', 'A'..'Z');

sub to_base_b { # Converts decimal number to base b string
    my($dec, $base) = @_;
    my @digits;
    while ($dec) {
        unshift @digits, (DIGITS)[$dec % $base];
        $dec = int($dec/$base);
    }
    return join "", @digits;
}

sub is_brazilian {
    my $n = shift;
    return 1 if $n % 2 == 0 and $n >= 8;
    return 0 if $n <= 3;
    for my $base (2..$n-2) {
        return 1 if to_base_b($n, $base) =~ /^(\d)\1+$/;
    }
    0;
}

say "Brazilian numbers less than or equal to 36 are:";
for my $m (1..36) {
    print "$m " if is_brazilian($m);
}
say "";

This program displays the following output:

$ perl brazilian_number.pl
Brazilian numbers less than or equal to 36 are:
7 8 10 12 13 14 15 16 18 20 21 22 24 26 27 28 30 31 32 33 34 35 36

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on April 3, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.