laurent_r

These are some answers to the Week 158 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a couple of days from now (on April 3, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Additive Primes

Write a script to find out all Additive Primes <= 100.

Additive primes are prime numbers for which the sum of their decimal digits are also primes.

Output

2, 3, 5, 7, 11, 23, 29, 41, 43, 47, 61, 67, 83, 89

Additive Primes in Raku

Using the is-prime (used twice), comb, and sum methods, this task can be solved in Raku with a simple one-liner:

say join ", ",  grep { .is-prime and .comb.sum.is-prime }, 1..100;

This script displays the following output:

$ raku ./add-prime.raku
2, 3, 5, 7, 11, 23, 29, 41, 43, 47, 61, 67, 83, 89

Additive Primes in Perl

Perl doesn’t have a built-in is_prime subroutine, so we implement it. In this case, we only need to check primality of integers smaller than than 100, which means that we need to check divisibility by primes smaller than 10, i.e. only four integers (2, 3, 5, 7).

use strict;
use warnings;
use feature "say";

my @small_primes = (2, 3, 5, 7);

sub is_prime {
    my $n = shift;
    for my $p (@small_primes) {
        return 1 if $p == $n;
        return 0 if $n % $p == 0;
    }
    return 1;
}

for my $n (grep {is_prime $_} 2..100) {
    my $sum = 0;
    $sum += $_ for split '', $n;
    print "$n " if is_prime $sum;
}
say "";

This script displays the following output:

$ perl ./add-prime.pl
2 3 5 7 11 23 29 41 43 47 61 67 83 89

Task 2: First Series Cuban Primes

Write a script to compute first series Cuban Primes <= 1000. Please refer to this Wikipedia page for more informations.

Output:

7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919.

A Cuban prime is a prime number that is also a solution to one of two different specific equations involving differences between third powers of two integers x and y.

The equation for the first series Cuban Primes is:

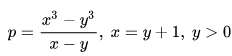
Replacing x with y + 1 in the first part of this equation leads to the following simplified formula: 3 y² + 3 y + 1.

Note that these numbers have apparently nothing to do with Cuba: their name is derived from the role cubes (third powers) play in the equations.

First Series Cuban Primes in Raku

We simply compute 3 y² + 3 y + 1 for successive integer values of y and print out those that yield prime integer result:

for 1..Inf -> $n {
    my $p = 3 * $n ** 2 + 3 * $n + 1;
    last if $p > 1000;
    print "$p, " if $p.is-prime;
}
say " ";

This program displays the following output:

$ raku ./cuban.raku
7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919,

First Series Cuban Primes in Perl

We update the is_prime subroutine of the previous task to work until 1000, so that we use primes between 2 and the square root of 1000, i.e. between 3 and 31. Besides that, this program is essentially a port to Perl of the Raku program above:

use strict;
use warnings;
use feature "say";

my @small_primes = (2, 3, 5, 7, 11,13, 17, 19, 23, 29, 31);

sub is_prime {
    my $n = shift;
    for my $p (@small_primes) {
        return 1 if $p == $n;
        return 0 if $n % $p == 0;
    }
    return 1;
}

for my $n (1..50) {
    my $p = 3 * $n ** 2 + 3 * $n + 1;
    last if $p > 1000;
    print "$p, " if is_prime $p;
}
say " ";

This program displays the following output:

$ perl ./cuban.pl
7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919,

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on April 10, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.