laurent_r

These are some answers to the Week 165 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

This week, Task 1 and part of Task 2 relate to Scalable Vector Graphics (SVG). I’d been using SVG a very long time ago and certainly didn’t remember any of the details. So, in my first blog relating to PWC 165, I stated that I didn’t have time for that and covered only the part of the challenge not related to SVG. I also said that, in the event that I find some time over the weekend, I might come back and fulfill the SVG part. I thought at the time that this was rather unlikely, but I was finally able to cover the SVG part, at least in Raku.

Task 1: Scalable Vector Graphics (SVG)

Scalable Vector Graphics (SVG) are not made of pixels, but lines, ellipses, and curves, that can be scaled to any size without any loss of quality. If you have ever tried to resize a small JPG or PNG, you know what I mean by “loss of quality”! What many people do not know about SVG files is, they are simply XML files, so they can easily be generated programmatically.

For this task, you may use external library, such as Perl’s SVG library, maintained in recent years by our very own Mohammad S Anwar. You can instead generate the XML yourself; it’s actually quite simple. The source for the example image for Task #2 might be instructive.

Your task is to accept a series of points and lines in the following format, one per line, in arbitrary order:

Point: x,y

Line: x1,y1,x2,y2

Example:

53,10
53,10,23,30
23,30

Then, generate an SVG file plotting all points, and all lines. If done correctly, you can view the output .svg file in your browser.

Scalable Vector Graphics (SVG) in Raku

I created two subroutines, make-point and make-line, to create the necessary data structures. The last item of the @input has three parts and should generate a warning, since input items should have either 2 or 4 parts.

Note that SVG probably includes a scaling factor, but I couldn’t find any information about it. So I rolled out my own \SCALE scaling factor to make the output larger and more readable.

use SVG;
my \SCALE = 5;

my ( @points, @lines);
my @input = <53,10  53,10,23,30  23,30  34,35,36>;
for @input -> $val {
    my @items = split /','/, $val;
    if @items.elems == 2 {
        make-point(@items)
    } elsif @items.elems == 4 {
        make-line(@items);
    } else { 
        note "Error on item ", @items;
    }
}

say ( SVG.serialize(svg => [ width => 500, height => 500, |@points, |@lines ] ));

sub make-point (@dots) {
    @dots = map { $_ * SCALE }, @dots;
    my $point = circle =>  
        [ cx => @dots[0],
          cy => @dots[1],
          r => 3,
          fill => 'forestgreen' ];
    push @points, $point;
}

sub make-line (@dots) {
    @dots = map { $_ * SCALE }, @dots;
    my $line = line => 
        [ x1 => @dots[0],
          y1 => @dots[1],
          x2 => @dots[2],
          y2 => @dots[3],
          stroke => 'navy' ];
    push @lines, $line;
}

The SVG output, slightly reformatted for better readability, is as follows:

<svg xmlns="http://www.w3.org/2000/svg" xmlns:svg="http://www.w3.org/2000/svg" 
xmlns:xlink="http://www.w3.org/1999/xlink" width="500" height="500">
<circle cx="265" cy="50" r="3" fill="forestgreen" />
<circle cx="115" cy="150" r="3" fill="forestgreen" />
<line x1="265" y1="50" x2="115" y2="150" stroke="navy" /></svg>

And this is a graphical rendering of it:

Scalable Vector Graphics (SVG) in Perl

In Perl, for a change, we will write directly the SVG data.

use strict;
use warnings;
use feature "say";
use constant SCALE => 5;

my ( @points, @lines);
my $out = qq{<svg xmlns="http://www.w3.org/2000/svg" xmlns:svg="http://www.w3.org/2000/svg" 
xmlns:xlink="http://www.w3.org/1999/xlink" width="500" height="500">\n};
my @input = qw<53,10 53,10,23,30  23,30  34,35,36>;
for my $val (@input) {
    my @items = split /,/, $val;
    # say "@items";
    if (@items == 2) {
        make_point(@items)
    } elsif (@items == 4) {
        make_line(@items);
    } else { 
        warn "Error on item ", @items;
    }
}
$out .= "</svg>";
say $out;

sub make_point {
    my @dots = map $_ * SCALE, @_;
    my $point = qq{<circle cx= "$dots[0]" cy="$dots[1]" r="3" fill="forestgreen"/>\n};
    $out .= $point;
}

sub make_line {
    my @dots = map $_ * SCALE, @_;
    my $line = qq{<line x1="$dots[0]" y1="$dots[1]" x2="$dots[2]" y2="$dots[3]" };
    $line .= qq{stroke="navy" />\n};
    $out .= $line
}

This program displays the following SVG output:

<svg xmlns="http://www.w3.org/2000/svg" xmlns:svg="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink" width="500" height="500">
<circle cx= "265" cy="50" r="3" fill="forestgreen"/>
<line x1="265" y1="50" x2="115" y2="150" stroke="navy" />
<circle cx= "115" cy="150" r="3" fill="forestgreen"/>
</svg>

And this is the graphgical rendering:

Task 2: Line of Best Fit

When you have a scatter plot of points, a line of best fit is the line that best describes the relationship between the points, and is very useful in statistics. Otherwise known as linear regression, here is an example of what such a line might look like:

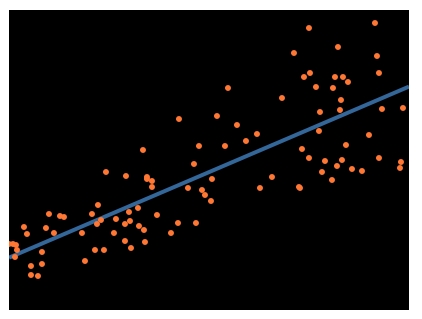
The method most often used is known as the least squares method, as it is straightforward and efficient, but you may use any method that generates the correct result.

Calculate the line of best fit for the following 48 points:

333,129  39,189 140,156 292,134 393,52  160,166 362,122  13,193
341,104 320,113 109,177 203,152 343,100 225,110  23,186 282,102
284,98  205,133 297,114 292,126 339,112 327,79  253,136  61,169
128,176 346,72  316,103 124,162  65,181 159,137 212,116 337,86
215,136 153,137 390,104 100,180  76,188  77,181  69,195  92,186
275,96  250,147  34,174 213,134 186,129 189,154 361,82  363,89

Using your rudimentary graphing engine from Task #1, graph all points, as well as the line of best fit.

So, Task 2 is about line of best fit or linear regression.

If we consider a cloud of n points with coordinates (x, y), the line of best fit is defined as follows:

The equation for the slope m is:

    n * sum(xy) - sum(x) * sum(y)
m = -----------------------------
    n * sum(x²) - sum(x) * sum(x)

The y-intercept (i.e. value of y on the vertical axis, when x = 0) b is:

    sum(y) - m * sum(x)
b = -------------------
           n

The equation of the line is:

y = mx + b

Line of Best Fit in Raku

The following program is an application of the explanations above. We split the input string on spaces and on commas, to get an array of (x, y) values. The lsm subroutine applies the above least square method formulas to find the slope and intercept. Note that for displaying line of best fit equation, we had to handle two different cases, depending on whether the intercept is positive or negative. Otherwise, for a negative intercept, we would display the line equation as follows:

The equation of the line of best fit is: y = 1.00 x + -1.00

which is not satisfactory.

Also note the use of the » hyper operator when reading the input data to apply the second split to each of the values returned by the first split.

Besides, we reuse the make-point and make-line subroutines created above (slightly modified) for preparing the SVG output.

use SVG;
my \SCALE = 1;

my $input =
   '333,129  39,189 140,156 292,134 393,52  160,166 362,122  13,193
    341,104 320,113 109,177 203,152 343,100 225,110  23,186 282,102
    284,98  205,133 297,114 292,126 339,112 327,79  253,136  61,169
    128,176 346,72  316,103 124,162  65,181 159,137 212,116 337,86
    215,136 153,137 390,104 100,180  76,188  77,181  69,195  92,186
    275,96  250,147  34,174 213,134 186,129 189,154 361,82  363,89';

my @points = $input.split(/\s+/)>>.split(/','/);
my (@dots, @lines);
make-point($_) for @points;
my ($slope, $intercept) = lsm(@points);
say "Slope: $slope, intercept = $intercept";
my $sign = $intercept < 0 ?? '-' !! '+';
printf "The equation of the line of best fit is: y = %.2f x %s %.2f \n\n", $slope, $sign, $intercept.abs;
# compute some arbitrary values for the line - say for x = 400
my $x = 400;
my $y = $slope * $x + $intercept;
make-line([0, $intercept, $x, $y]);
say ( SVG.serialize(svg => [ width => 500, height => 500, |@dots, |@lines ]));

sub lsm (@points) {
    my ($s-x, $s-y, $s-xy, $s-x2) = 0 xx 4;
    for @points -> $point {
        my ($x, $y) = $point[0, 1];
        # say "$x $y";
        $s-x += $x;
        $s-y += $y;
        $s-xy += $x * $y;
        $s-x2 += $x ** 2;
    }
    my $n = @points.elems;
    my $slope = ($n * $s-xy - $s-x * $s-y) / ($n * $s-x2 - $s-x ** 2);
    my $intercept = ($s-y - $slope * $s-x) / $n;
    return $slope, $intercept;
}

sub make-point (@points is copy) {
    @points = map { $_ * SCALE }, @points;
    my $point = circle =>  
        [ cx => @points[0],
          cy => @points[1],
          r => 3,
          fill => 'forestgreen' ];
    push @dots, $point;
}

sub make-line (@dots) {
    @dots = map { $_ * SCALE }, @dots;
    my $line = line => 
        [ x1 => @dots[0],
          y1 => @dots[1],
          x2 => @dots[2],
          y2 => @dots[3],
          stroke => 'navy' ];
    push @lines, $line;
}

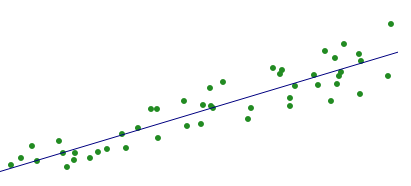
This program displays the following output:

$ ./raku lsm2.raku
Slope: -0.2999565, intercept = 200.132272536
The equation of the line of best fit is: y = -0.30 x + 200.13

<svg xmlns="http://www.w3.org/2000/svg" xmlns:svg="http://www.w3.org/2000/svg" 
xmlns:xlink="http://www.w3.org/1999/xlink" width="500" height="500">
<circle cx="333" cy="129" r="3" fill="forestgreen" /><circle cx="39" cy="189" r="3" fill="forestgreen" />
<circle cx="140" cy="156" r="3" fill="forestgreen" /><circle cx="292" cy="134" r="3" fill="forestgreen" />
<circle cx="393" cy="52" r="3" fill="forestgreen" /><circle cx="160" cy="166" r="3" fill="forestgreen" />
<circle cx="362" cy="122" r="3" fill="forestgreen" /><circle cx="13" cy="193" r="3" fill="forestgreen" />
<circle cx="341" cy="104" r="3" fill="forestgreen" /><circle cx="320" cy="113" r="3" fill="forestgreen" />
<circle cx="109" cy="177" r="3" fill="forestgreen" /><circle cx="203" cy="152" r="3" fill="forestgreen" />
<circle cx="343" cy="100" r="3" fill="forestgreen" /><circle cx="225" cy="110" r="3" fill="forestgreen" />
<circle cx="23" cy="186" r="3" fill="forestgreen" /><circle cx="282" cy="102" r="3" fill="forestgreen" />
<circle cx="284" cy="98" r="3" fill="forestgreen" /><circle cx="205" cy="133" r="3" fill="forestgreen" />
<circle cx="297" cy="114" r="3" fill="forestgreen" /><circle cx="292" cy="126" r="3" fill="forestgreen" />
<circle cx="339" cy="112" r="3" fill="forestgreen" /><circle cx="327" cy="79" r="3" fill="forestgreen" />
<circle cx="253" cy="136" r="3" fill="forestgreen" /><circle cx="61" cy="169" r="3" fill="forestgreen" />
<circle cx="128" cy="176" r="3" fill="forestgreen" /><circle cx="346" cy="72" r="3" fill="forestgreen" />
<circle cx="316" cy="103" r="3" fill="forestgreen" /><circle cx="124" cy="162" r="3" fill="forestgreen" />
<circle cx="65" cy="181" r="3" fill="forestgreen" /><circle cx="159" cy="137" r="3" fill="forestgreen" />
<circle cx="212" cy="116" r="3" fill="forestgreen" /><circle cx="337" cy="86" r="3" fill="forestgreen" />
<circle cx="215" cy="136" r="3" fill="forestgreen" /><circle cx="153" cy="137" r="3" fill="forestgreen" />
<circle cx="390" cy="104" r="3" fill="forestgreen" /><circle cx="100" cy="180" r="3" fill="forestgreen" />
<circle cx="76" cy="188" r="3" fill="forestgreen" /><circle cx="77" cy="181" r="3" fill="forestgreen" />
<circle cx="69" cy="195" r="3" fill="forestgreen" /><circle cx="92" cy="186" r="3" fill="forestgreen" />
<circle cx="275" cy="96" r="3" fill="forestgreen" /><circle cx="250" cy="147" r="3" fill="forestgreen" />
<circle cx="34" cy="174" r="3" fill="forestgreen" /><circle cx="213" cy="134" r="3" fill="forestgreen" />
<circle cx="186" cy="129" r="3" fill="forestgreen" /><circle cx="189" cy="154" r="3" fill="forestgreen" />
<circle cx="361" cy="82" r="3" fill="forestgreen" /><circle cx="363" cy="89" r="3" fill="forestgreen" />
<line x1="0" y1="200.132272536" x2="400" y2="80.149672431" stroke="navy" />
</svg>

And this is a graphiical rendering of it:

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on May 29, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.