Ovid

I recently posted about Failing your way to success with A/B testing and I was pleasantly surprised about the very active feedback.

One issue which was raised was by Steffan Mueller (one of my colleagues at booking.com and a brilliant guy) is a common concern:

What I am most afraid of in the kind of A/B testing I've seen is that it seems very prone to getting stuck in local minima. In that image, imagine you're in the place marked with the red arrow. Taking small steps and adjusting for the test result each time, you're never going to reach the optimal place (blue arrow) since once you're in the local minimum, all small steps you can take actually produce a worse result.

Aristotle raised a similar concern and I think it's important enough to address up front.

I'd like to invert that and talk instead about local maxima and why you really don't have to worry about it too much.

Consider the following image. Let's imagine that the horizontal axis represents a theoretical "shape" to your Web site representing some combination of features and the vertical scale represents the conversion rate. In other words, the vertical scale represents the percentage of customers who purchased something (though there might be other conversion metrics). Ignore the numbers on the graphs; it's the shape which is important for this explanation.

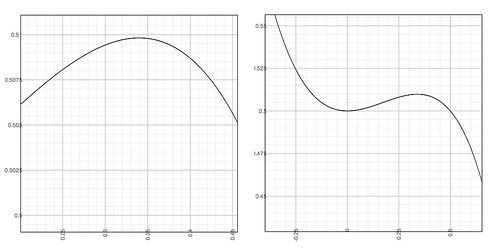Local Maxima of y = (x^3-1)/(x^2-2)

Imagine your web site is converting customers at the left most point of the left graph. You'd be very pleased to get to the topmost point on that graph because more conversion generally means more money. Then you have someone come up and claim that actually, the rightmost graph is more accurate and you can get a higher conversion rate. The problem is that A/B testing involves a small series of changes and if you get to the local maxima on the leftmost graph, you may find that you can't create small A/B tests and make a large enough change to break out of that local maxima.

But is this a problem? First, let consider another case where local maxima (and minima) are important.

As some of you are aware, I have a neural net module on the CPAN. One way of training the neural network is to take a known good data set, randomly partition it and use one partition for the training and the other partition for the verification. You set all of the neurons' synapses to have random weights and keep running your training data through the network until it "learns" how to predict accurate results.

However, let's say you're using this for sales projections. You may very well find that there's a strange limit to your projections even though your sales are beyond that limit. You may very well have accidentally trained your network into a local maxima beyond which it cannot predict sales results. How do you fix this? You take another data set, randomly partition it, create a new network with randomly seeded weights on the synapses and retrain. You may have to do this several times until you get valid results.

Why do you take this approach to neural networks? For almost the same reason you may hit local maxima with A/B testing: you can't know how the answers are arrived at. Though there are data mining tools for neural networks, they still can't tell you why something happened. However, they offer you something A/B testing can't: they can give you a hint at the landscape in which your data lives.

For A/B testing, you may try and rerun tests with randomly partitioned data and see if you get better results but it probably won't work because you can't know how humans are going to respond to a different set of experiments.

What's worse, you can't randomly reseed "synapses" every time this happens because this is the metaphorical equivalent of a Web site relaunch. Not only can this be expensive, it's clearly an undiggnified way of flailing your way to a different outcome and as many companies who have relaunched their Web sites have found, lacking a clear and undeniably compelling reason why you should relaunch, you may just kill your company. Perhaps even worse, even if you succeed, you won't always know what did and did not make things better. I stress this point because it's critically important to remember this about A/B testing: you may know what happened, but you're guessing as to why.

However, this really isn't a problem. First, remember that I'm talking about this in the context of a business which needs to succeed. What does the business do without A/B testing? They have account managers to negotiate better contracts. They have salespeople to attract new customers. They have a marketing department to attract new customers. They have office managers to keep down supply costs. They have IT departments to improve inventory control. You have so many tools to grow the business that if you are trying to rely solely on A/B testing, you're insane! Further, if you go to marketing and try to convince them that they might be trapped in an unknowable local maxima, they can simply respond "that's nice. We've increased conversion 50%" and they're right. Focus on what you can achieve, not on what can't.

But let's say, hypothetically, with a huge amount of market research you can be reasonably certain that you are in a local maxima and you might be able to break out of it. The counter-intuitive response is that this might be counter-productive.

Your business likely has multiple conversion funnels. A typical one might look like this:

1. Customer clicks on an advertisement
2. They get to your Web site and search for a product
3. They click "Buy now!"
4. They enter their details and purchase the product

At each step of this process you get fewer customers, hence the "funnel" metaphor. Each step has a binary (yes/no) distribution of customers "converting" for that step. Let's say that you suspect you're in a local maxima for step 3, the "Buy Now!" stage. You don't actually know the "shape" of your customer's behaviour at this point relative to the other steps. Sure, you might try to have a massive research project to find out what's going on, but at the same time you're probably running A/B tests on the other stages in the funnel. As a result, you're changing the shape of your landscape. You can try to figure out whether you have a local maxima, but business charges ahead and changes the landscape enough that your research is invalid. Thus, A/B testing should be focusing on all stages of the funnel, constantly trying to improve them in small, inexpensive, low-risk steps. Your local maxima is relative to a constantly changing landscape and figuring out if it exists is not a small, inexpensive and low-risk step. You can't know the answer anyway, so focus on what you can do and not what you can't.

This, incidentally, is why you often want to keep various A/B tests lying around so that when you think the landscape has changed enough that you retest critical tests to find out if you have the same benefit.

Remember: A/B testing can offer great benefits, but they require a lot of thought and business knowledge to understand why you get the results you do. You must, must, must think about what's going on and not simply follow the numbers blindly. That being said, while they can tremendously improve your bottom line, they also have to be used in conjunction with the rest of your business strategy.

As an aside, I should mention that one possible way of minimizing the local maxima problem is multi-variate testing. I'll explain what it is and some of the serious inherent problems in a later post.