To compute a constant of calculus(A treatise on multiple ways)
𝑒 is for economics
The first task of the
21st Weekly Challenge
was a very old one:
to find (what would eventually become known as) Euler’s number.
The story starts back in 1683 with Jacob Bernoulli, and his investigation of the mathematics of
loan sharking. For example, suppose you offered a one-year loan of $1000 at 100% interest,
payable annually. Obviously, at the end of the year the markclient has to pay
you back the $1000, plus ($1000 × 100%) in interest...so you now have $2000. What can I say?
It’s a sweet racket!
But then you get to thinking: what if the interest got charged every six months? In that case,
after six months they already owe you $500 in interest ($1000 x 100% × 6∕12), on which amount
you can immediately start charging interest as well! So after the final six months they now owe
you the original $1000 plus the first six months interest, plus the second six months interest,
plus the second six months interest on the first six months interest: $1000 + ($1000 × 50%)
+ ($1000 × 50%) + ($1000 × 50% × 50%). Which is $2250.
Which is an even sweeter racket.
Of course it’s easier to calculate what they owe you mathematically: $1000 × (1 + ½)2
The added ½ comes from charging half the yearly interest every six months.
The power of 2 comes from charging that interest twice a year.
But why stop there? Why not charge the interest monthly instead? Then you get back the
original $1000, plus $83.33 interest (i.e. 1∕12 of $1000) for the first month,
plus $90.28 interest for the second month (i.e. 1∕12 of: $1000 + $83.33),
plus $97.80 interest for the third month (i.e. 1∕12 of: $1000 + $83.33 + $90.28),
et cetera. In other words: $1000 x (1 + 1∕12)12
or $2613.04. Nice.
If we charged interest daily, we’d get back $2714.57 (i.e. $1000 x (1 + 1∕365)365).
If we charged it hourly, we’d get back $2718 (i.e. $1000 x (1 + 1∕8760)8760).
If we charged by the minute, we’d get back $2718.27 (i.e. $1000 x (1 + 1∕525600)525600).
Bernoulli then asked the obvious question: what’s the absolute most you could squeeze outa
deese pidgeons? Just how much would you get back if you charged interest continuously?
In other words, what is the multiplier on your initial $1000 if you charge and accumulate interest
at every instant? Or, mathematically speaking, what is the limit as x→∞ of
(1 + 1∕x)x?
The answer to that question is the transcendental numeric constant 𝑒:
2.7182818284590452353602874713526624977572470936999595749669...
Which is named after Leonhard Euler instead of Jacob Bernoulli because (a) Euler was the first person to use it explicitly in a published scientific paper, and (b) it really does make everything so much simpler if we just name everything after Euler.
𝑒 is for elapsed
So, given that 𝑒 is the limit of (1 + 1∕x)x, for increasingly large values of x, we could compute progressively more accurate approximations of the constant with just:
for 1, 2, 4 ... ∞ -> \x {
say (1 + x⁻¹) ** x
}
...which produces:
2
2.25
2.441406
2.565784514
2.6379284973666
2.676990129378183
2.697344952565099
2.7077390196880207
2.7129916242534344
2.7156320001689913
2.7169557294664357
2.7176184823368796
2.7179500811896657
2.718115936265797
2.7181988777219708
2.718240351930294
2.7182610899046034
2.7182714591093062
2.718276643766046
2.718279236108013
⋮
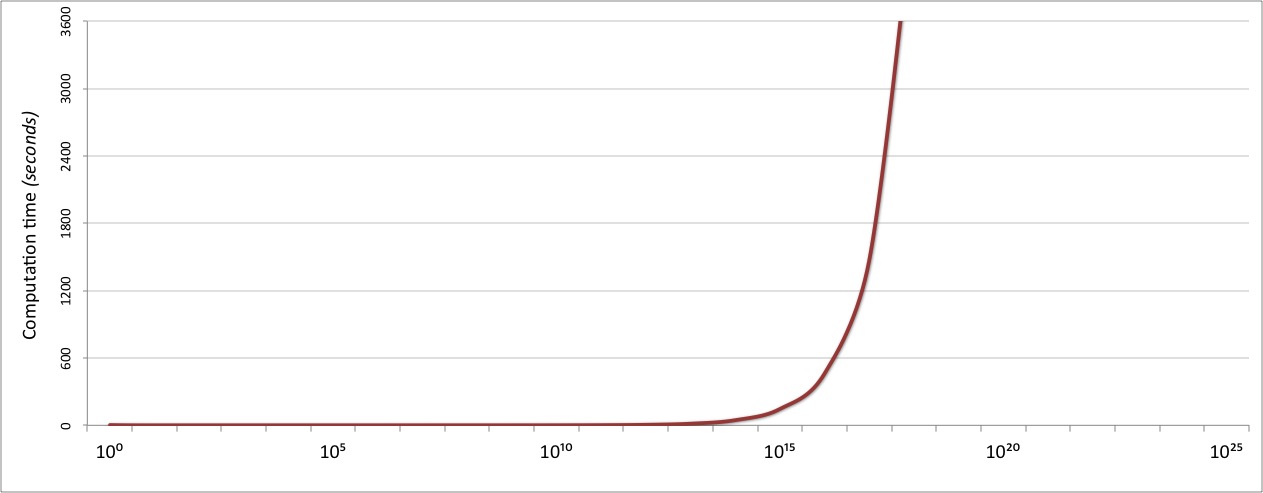
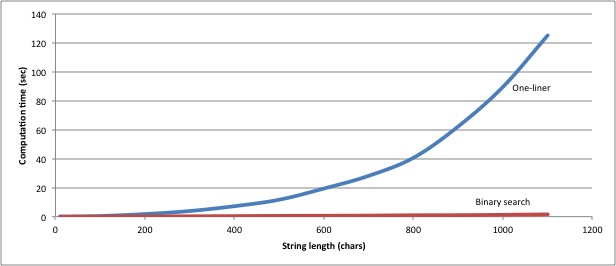
That’s an easy solution, but not a great one. After 20 iterations, at N=524288,
it’s still only accurate to five decimal places (
More importantly, it’s a slow solution. How slow?
Let’s whip up an integrated timing mechanism to tell us:
# Evaluate the block and add timing info to the result...
sub prefix:<timed> (Code $block --> Any) {
# Represent added timing info...
role Timed {
# Store the actual timing...
has Duration $.timing;
# When stringified, append the timing...
my constant FORMAT = "%-20s [%.3f𝑠]";
method Str { sprintf FORMAT, callsame, $.timing }
method gist { self.Str }
}
# Evaluate the block, mixing timing info into result...
return $block() but Timed(now - ENTER now);
}
Here we create a new high-precedence prefix operator: timed.
It’s an genuine operator, even though its symbol is also a proper identifier.
We could just as easily have named it with an ASCII or Unicode
symbol if we’d wanted to:
# Vaguely like a clock face...
sub prefix:« (<) » (Code $block --> Any) {…}
# Exactly like a stopwatch...
sub prefix:« ⏱ » (Code $block --> Any) {…}
Even without the fancy symbols, we still want an operator rather than a subroutine because
the precedence of a regular subroutine call is too low. If timed had been declared as
sub timed we wouldn’t be able to place a timed block in a surrounding argument list,
as the call to timed would attempt to gobble up all the following arguments, and then
discover it is only allowed one:
say timed { expensive-func() }, " finished at ", now;
# Too many positionals passed; expected 1 argument but got 3
# in sub timed at demo.p6 line 5
Making timed a prefix operator allows the compiler to know that it can
only ever take a single argument, so inline calls like the one above work fine.
Note that, as we’re feeling in need of a little extra discipline today, we’re going to make use of Raku’s type system and strictly type every variable and parameter we use. Of course, because Raku’s static typing is gradual, the code would still work exactly the same if we later removed every one of these type declarations...except then the compiler would not be able to protect us quite so well from our own stupidity.
The timed operator takes a Code object as its argument, executes it ($block()),
augments the result with extra timing information, and returns the augmented result,
which can be of any type (--> Any).
That timing information is added to the block’s result by mixing into the returned object
some extra capabilities defined by a generic class component (a
role) named Timed.
The role confers the ability to store and access a duration (has Duration $.timing),
as well as methods for enhancing how a timed object is stringified and printed (method Str
and method gist). The overridden .Str method calls the object's original version
of
the same method (callsame) to do the actual work, then appends the timing information
to
it, neatly formatted in a sprintf. The overridden .gist just reuses .Str.
The most interesting feature is that, when we add the timing information to the result
of the block (but Timed(...)), we calculate the duration of the block’s execution
by subtracting the instant after the block executes (now) from the current
instant when the surrounding subroutine was entered (ENTER now). Prefixing any
expression with ENTER sets up a “phaser”
(yeah, we know: we’re incurable geeks).
A phaser is a block or thunk
that executes when the surrounding block is entered. The ENTER then remembers the value
generated by the thunk, and evaluates to it when the surrounding code executes: in this
case, when it tries to subtract the value of the ENTER from the value of now.
You can use this same technique anywhere in Raku, as a handy way to time any particular block
of code. You can also use other phasers (such as LEAVE, which executes when control leaves
the surrounding block) to inline the entire operation into an easily pasteable snippet. For
example, to time each iteration of a for loop, you could add a single line to the start of
the loop block:
for @values -> $value {
LEAVE say "$value took ", (now - ENTER now), " seconds";
do-something-expensive-with($value);
do-something-else-protracted-with($value);
do-the-last-costly-thing-with($value);
}
So now we can easily time any block of code, simply by prefixing the block with the
timed operator. And when we do that in our calculation loop:
for 1, 2, 4 ... ∞ -> \x {
say timed { (1 + x⁻¹) ** x }
}
...we find that we’re going to be waiting an exponentially long time for better accuracy:
⋮
2.7176184823368796 [0.001𝑠]
2.7179500811896657 [0.002𝑠]
2.718115936265797 [0.011𝑠]
2.7181988777219708 [0.051𝑠]
2.718240351930294 [0.241𝑠]
2.7182610899046034 [1.123𝑠]
2.7182714591093062 [4.802𝑠]
2.718276643766046 [21.468𝑠]
2.718279236108013 [106.543𝑠]
⋮
Clearly, we need a much better algorithm.
𝑒 is for extrema
In 100 Great Problems of Elementary Mathematics Heinrich Dörrie shows that, just as (1+1∕x)x is the lower bound on 𝑒 as x → ∞, so (1 + 1∕x)x+1 is the upper bound. So we can get a much better approximation of 𝑒 for the same value of N by taking the average of those two bounding values:
for 1, 2, 4 ... ∞ -> \x {
say timed {
½ × sum (1 + x⁻¹)**(x),
(1 + x⁻¹)**(x+1)
}
}
which produces:
3 [0.001𝑠]
2.8125 [0.000𝑠]
2.746582 [0.000𝑠]
2.72614604607 [0.000𝑠]
2.7203637629093063 [0.000𝑠]
2.7188181001497167 [0.001𝑠]
2.718417960007014 [0.001𝑠]
2.718316125233677 [0.000𝑠]
2.7182904360195543 [0.000𝑠]
2.718283984544156 [0.000𝑠]
2.7182823680062143 [0.000𝑠]
2.718281963411669 [0.001𝑠]
2.718281862205436 [0.005𝑠]
2.7182818368966726 [0.021𝑠]
2.718281830568581 [0.101𝑠]
2.718281828986445 [0.456𝑠]
2.7182818285908974 [2.171𝑠]
2.7182818284920085 [9.628𝑠]
2.718281828467286 [46.717𝑠]
2.718281828461105 [206.456𝑠]
⋮
That’s ten correct decimal digits (
𝑒 is for evaluation
It looks like we’re going to need to try a lot of different techniques, over a wide
range of values. So it would be handy to have a simpler way of specifying a series of tests like
these,
and a better way of seeing how well or poorly they perform.
So we’re going to create a framework that will let us test various techniques more simply, like so:
#| Bernoulli's limit
assess -> \x { (1 + x⁻¹)**(x) }
#| Dörrie's bounds
assess -> \x {
½ × sum (1 + x⁻¹)**(x),
(1 + x⁻¹)**(x+1)
}
Or, if we prefer, to specify a more appropriate range of trial values than just 1..∞, like so:
#| Dörrie's bounds
assess -> \x=(1,10,100...10⁶) {
½ × sum (1 + x⁻¹)**(x),
(1 + x⁻¹)**(x+1)
}
Either way, the assess function will calculate each result, determine when to give up on
slow computations, tabulate the outcomes, colour-code their accuracy, and print them out neatly
labelled, like so:
[1] Bernoulli's limit (x = 1):
[4] Dörrie's bounds (x = 1):
To implement all that, we start with a generic class component (i.e. another role)
suitable for storing, vetting, and formatting whatever the data we’re collecting:
# Define a new type: Code that takes exactly one parameter...
subset Unary of Code where *.signature.params == 1;
# Reportable values, assessed against a target...
role Reportable [Cool :$target = ""]
{
# Track reportable objects and eventually display them...
state Reportable @reports;
END @reports».display: @reports».width.max;
# Add reportable objects to tracking list, and validate...
submethod TWEAK (Unary :$check = {True}) {
@reports.push: self;
$check(self);
}
# Each report has a description and value...
has Str $.desc handles width => 'chars';
has Cool $.value handles *;
# Display the report in two columns...
method display (Int $width) {
printf "%*s: %s\n", $width, $!desc, &.assess-value;
}
# Colour-code the value for display...
method assess-value () {
# Find leading characters that match the target...
my Int $correct
= ($!value ~^ $target).match( /^ \0+/ ).chars;
# Split the value accordingly...
$!value.gist ~~ /^ $<good> = (. ** {$correct})
$<bad> = (\S*)
$<etc> = (.*)
/;
# Correct chars: blue; incorrect chars: red...
use Terminal::ANSIColor;
return colored($<good>.Str, 'blue')
~ colored($<bad>.Str, 'red')
~ $<etc>
}
}
We start by creating a new subtype (subset Unary)
of the built-in Code type (i.e. the general type of blocks, lambdas, subroutines, etc.)
This new subtype requires that the
Code object must take exactly one argument (where *.signature.params == 1).
Because (almost) everything in Raku is an object, it’s easy for the language to provide
these types of detailed introspection
methods on values, variables,
types, and code.
Next we create a pluggable component (role Reportable) for building classes that
generate self-organizing reports. This role is
parameterized
to take a named value (:$target) that will subsequently be used to assess the accuracy of
individual values being reported. That target value is specified to be of type
Cool, which allows it to be a string, a number, a
boolean, a duration, a hash, a list, or any other type automatically convertible to a
string or number. This type constraint will ensure that any value reported will later be
able to be assessed correctly. The :target parameter is optional; the default target
being the empty string.
The Reportable role is going to automatically track all reportable objects for us...and then
generate the aggregrated report at the end of the program. So we declare a shared variable
to hold each report (state Reportable @reports), with a type specifier that requires
each element of the array be able to perform the Reportable role. To ensure that the
reports are eventually printed, we add an END phaser:
END @reports».display: @reports».width.max;
At the end of execution, this statement calls the .display method of each report
(@reports».display), passing it the maximum width of any report description
(@reports».width.max) so that it can format the report into two clean columns.
To accumulate these reports, we arrange for each Reportable object to automatically
add itself to the shared @reports array, when it is constructed...by declaring a
TWEAK submethod. A submethod
is a class-specific, non-inherited method, suitable for specifying per-class initializers. The
TWEAK submethod is called automatically after an object is created: usually to adjust
its initial value, or to test its integrity in some way.
Here, we’re doing both: by having the submethod add each object to the report list
(@reports.push: self) and by applying any :check code passed to the constructor
($check(self)). This allows the user to pass in an arbitrary test during the constructor call
and have it applied to the object once that object is initialized. We’ll see shortly how
useful that can be.
Each report consists of a string description and a value that can be any Cool type, so we
need per-object attributes to store them. We declare them with the has keyword and a
“dot” secondary sigil
to make them public:
has Str $.desc;
has Cool $.value;
We also need to be able to access the string width of the description.
We could declare a method to provide that information:
method width { $.desc.chars }
But, as this is just forwarding a request from the Reportable object to the $.desc object
inside it, there’s a much easier way to achieve the same effect: we simply tell the
$.desc attribute that it should handle all object-level calls to .width by calling
its own .chars method. Like so:
has Str $.desc handles width => 'chars';
More significantly, we also need to be able to forward methods to the $.value attribute
(for example, to interrogate its .timing information). But as we don’t know what kind of
object the value may be in each case (apart from generically being Cool), we can’t know in
advance which methods we may need to forward. So we simply tell $.value to handle
whatever the surrounding object itself can’t, like so:
has Cool $.value handles *;
Now we just need to implement the .display method that the END phaser will use to output
each Reportable object. That method takes the width into which the description should be
formatted, and prints it out justified to that width using a printf. It also prints the value,
which is pre-processed using the .assess-value method.
.assess-value works out how well the value matches the target, by taking a
character-wise XOR between the two ($!value ~^ $target). For every character
(or digit in a stringified number) that matches, the XOR will produce a null character
('\0'). For every character that differs, the resulting XOR character will be something else.
So we can determine how many of the initial characters of the value match the target by
counting how many leading '\0' characters the XOR produces (.match( /^ \0+/ ).chars).
Then we just split the value string into three substrings using a regex,
colouring the leading matches blue and the trailing mismatches red,
using the Terminal::ANSIColor module.
Once we have the role available, we can build a couple of Reportable classes
suited to our actual data. Each result we produce will need to be assessed
against an accurate representation of 𝑒:
class Result
does Reportable[:target<2.71828182845904523536028747135266>]
{}
And we’ll also want to format our report with empty lines between the various
techniques we’re reporting, so we need a Reportable class whose .display
method is overridden to print only empty lines:
class Spacer
does Reportable
{
method display (Int) { say "" }
}
Finally we build the assess subroutine itself:
constant TIMEOUT = 3; # seconds;
# Evaluate a block over a range of inputs, and report...
sub assess (Unary $block --> Any) {
# Introspect the block's single parameter...
my Parameter $param = $block.signature.params[0];
my Bool $is-topic = $param.name eq '$_';
# Extract and normalize the range of test values...
my Any @values = do given try $param.default.() {
when !.defined && $is-topic { Empty }
when !.defined { 1, *×2 ... ∞ }
when .?infinite { .min, *×2 ... ∞ }
default { .Seq }
}
# Introspect the test description (from doc comments)...
my Str $label = "[$block.line()] {$block.WHY // ''}".trim;
# New paragraph in the report...
Spacer.new;
# Run all tests...
for @values Z $label,"",* -> ($value, $label) {
Result.new:
desc => "$label ($param.name() = $value)",
value => timed { $block($value) },
check => { last if .timing > TIMEOUT }
}
if !@values {
Result.new:
desc => $label,
value => timed { $block(Empty) }
}
}
The subroutine takes a single argument: a Code object that itself takes
a single parameter (which we enforce by giving the parameter the type Unary).
We immediately introspect that one parameter ($block.signature.params[0]),
which is (naturally) a Parameter object, and store it in a suitably typed variable
(my Parameter $param). We also need to know whether the parameter is the
implicit topic variable (a.k.a. $_), so we test for that too.
Once we have the parameter, we need to determine whether the caller gave it a default
value...which will represent the set of values for which we are to assess the code
in the block passed to assess. In other words, if the user writes:
assess -> \N=1..100 { some-function-of(N) }
...then we need to extract the default value (1..100) so we can iterate through
those values and pass each in turn into the block.
We can extract the parameter’s default value (if any!) by calling the appropriate
introspection method: $param.default, which will return another Code object
that produces the default value when called. Hence, to get the actual default
value we need to call .default, then call the code .default returns.
That is: $param.default.()
Of course, the parameter may not have a default value, in which case .default will
return an undefined value. Attempting the second call on that undefined value would
be fatal, so we make the attempt inside a try, which converts the exception
into yet another undefined value.
We then test the extracted default value to determine what it means:
when !.defined && $is-topic { Empty }
when !.defined { 1, *×2 ... ∞ }
when .?infinite { .min, *×2 ... ∞ }
default { .Seq }
If it’s undefined, then no default was specified, so we either use an empty list as our test
values (if the parameter is just the implicit topic, in which case it’s a parameterless
one-off trial), or else we use the endlessly doubling sequence 1, 2, 4 ... ∞. Using this
sequence instead of 1..∞ gives us reasonable coverage at every numeric order of
magnitude, without the tedium of trying every single possible value.
If the default was a range to infinity (when .?infinite), then we adjust it to similar
sequence of doubling values to infinity, starting at the same lower bound (.min). And if the
value is anything else, we just use it as-is, only converting it to a sequence (.Seq).
Once we have the test values, we need a description for the overall test. We could have simply
added a second parameter to assess, but the powerful introspective capabilities of Raku
offer a more interesting alternative...
We need to convey three pieces of information: the line number at which the call to assess
was made, a description of the trial being assessed, and the trial value for each trial.
However, to avoid uncomely redundancy, only the first trial needs to be labelled with the line
number and description; subsequent trials need only show the next trial value.
We can get the line number by introspecting the code block: $block.line()
But where can we get the description from?
Well...why not just read it directly from the comments?!
In Raku, any comment that starts with a vertical bar (i.e. #| Your comment here)
is a special form of documentation known as a
declarator block.
When you specify such a comment, its contents are automatically attached to the first
declaration following the comment. That might be a variable declared with a my, a
subroutine declared with a sub or multi, or (in this case) an anonymous block of
code declared between two braces.
In other words, when we write:
#| Bernoulli's limit
assess -> \x { (1 + x⁻¹)**(x) }
...the string "Bernoulli's limit" is automatically attached to the block that
is passed into assess. We could also put the documentation comment after the
block, by using #= as the comment introducer, instead of #|:
assess -> \x { (1+x⁻¹)**x } #= Bernoulli's limit
Either way, Raku’s advanced introspective facilities mean that we can retrieve that
documentation during program execution, simply by calling the block’s .WHY method
(because comments are supposed to tell you “WHY”, not “HOW”).
So we can generate our description by asking the block for its line number
and its documentation, making do with an empty string if no documentation comment was
supplied ("[$block.line()] {$block.WHY // ''}").
Now we’re ready to run our tests and generate the report. We start by inserting
an empty line into the report...by declaring a Spacer object. Then we iterate
through the list of values, and their associated labels, interleaving the two
with a “zip” operator (Z). The labels are the initial label we built earlier,
then an empty string, then a “whatever” (*), which tells the zip operator
to reuse the preceding empty string as many times as necessary to match the
remaining elements of @values. That way, we get the full label on the first
line of the trial, but no repeats of it thereafter.
The zip produces a series of two-element arrays: one value, one label. We then iterate through
these, building an appropriate Result object for each test:
Result.new:
desc => "$label ($param.name() = $value)",
value => timed { $block($value) },
check => { last if .timing > TIMEOUT }
The description for the report is the label, followed by the block’s parameter name
($param.name()) and the current trial value being passed to it on this iteration
($value). The value for the report is just the timed result of calling the block with the
current trial value passed to it (timed { $block($value) }).
But we also want to stop testing when the tests get too slow, so we pass the Result constructor
a check argument as well, which causes its TWEAK submethod to execute the check block once the
result has been added to the report list. Then we arrange for the check block to terminate
the surrounding for loop (i.e.last) if the timing of the new object exceeds our chosen
timeout. The call to .timing will be invoked on the Result object, which (not having a
timing method itself) will delegate the call to its $.value attribute, which we specified
to handle “whatever” methods the object itself can’t deal with.
The only thing left to do is to cover the edge-case where the user provides no test values
at all (i.e. when there are no @values to iterate through). That can happen either when an
explicit empty list of default values is passed to assert, or when the block passed in
doesn’t explicitly declare a parameter at all (and therefore defaults to the implicit topic
parameter: $_). In either case, we need to call the block exactly once, without any argument.
So if the array of test values has no elements (if @values.elems == 0),
we instantiate a single Result object, passing it the full label, and the timed result of
calling the block with a (literally) empty argument list:
if !@values {
Result.new:
desc => $label,
value => timed { $block(Empty) }
}
And we’re done. We now have an introspective and compact way of performing multiple trials on a block, across a range of suitable values, either explicit or inferred, with automatic timing of—and timeouts on—each trial.
So let’s get back to computing the value of 𝑒...
𝑒 is for eversion
The constant 𝑒 is associated with Jacob Bernoulli in another, entirely unrelated way. In his posthumous 1712 publication, Ars Conjectandi, Bernoulli explored the mathematics of binomial trials: random experiments in which the results are strictly binary: success or failure, true or false, yes or no, heads or tails.
One of the results of binomial theory has to do with the probability of extremely bad luck.
If we conduct a random binomial trial where the probability of success is
1∕k, then the probability of failure must be 1 -
1∕k. Which means that, if we repeat our same random trial
k times, then the probability of failing every time is (1 -
1∕k)k. As k grows larger, this probability
increases from zero (for k=1), to 0.25 (for k=2), to 0.296296296296... (for k=3), to
0.31640625 (for k=4), gradually converging on an asymptotic value of 0.36787944117144233...
(for k=∞). And the value 0.36787944117144233... is exactly
1∕𝑒.
Which means that (1 - 1∕k)-k must tend towards 𝑒 as k tends to ∞. So we can try:
#| Bernoulli trials
assess -> \k=2..∞ { (1 - k⁻¹) ** -k }
...which tells us:
[20] Bernoulli trials (k = 2):
Which, sadly, converges no faster than Bernoulli’s original loan sharking scheme.
𝑒 is for exclamation
Despite its disappointing performance, the Bernoulli trials approach highlights a useful idea. The constant 𝑒 appears in a great many other mathematical equations, all of which we could rearrange to produce a formula starting: 𝑒 = ...
For example, in 1733 Abraham de Moivre first
published
an asymptotic approximation for the factorial function, which (just a few days later!)
was refined
by James Stirling, after whom the approximation is now named.
That approximation is: n! ≅ √2πn × (n∕𝑒)n
with the approximation becoming more accurate as n becomes larger.
Rearranging that equation, we get: 𝑒 ≅ n/n√n!
For which we’re going to need both an n-th root operator and a factorial operator. Both of which are missing from standard Raku. Both of which are trivially easy to add to it:
# n-th root of x...
sub infix:<√> (Int $n, Int $x --> Numeric) is tighter( &[**] ) {
$x ** $n⁻¹
}
# Factorial of x...
sub postfix:<!> (Int $x --> Int) {
[×] 1..$x
}
The new infix √ operator is specified to have a precedence just higher than the existing
** exponentiation operator (is tighter( &[**] )). It simply raises the value after the
√ to the reciprocal of the value before the √.
The new postfix ! operator multiplies together all the numbers less than or equal to its
single argument (1..$x), using a reduction
by multiplication ([×]).
With those two new operators available, we can now write:
#| de Moivre/Stirling approximation
assess -> \n { n / n√n! }
Unfortunately, the results are less than satisfactory:
[30] de Moivre/Stirling approximation (n = 1):
This approach converges on 𝑒 even slower than the previous ones, and for the
first time
Raku has actually failed us when it comes to a numerical calculation. Those zeroes are
indicating that the compiler has been unable to take the 256th root of the factorial of 256.
Or deeper roots of higher numbers.
It computed the factorial itself (i.e. 8578177753428426541190822716812326251577815202 79485619859655650377269452553147589377440291360451408450375885342336584306 15719683469369647532228928849742602567963733256336878644267520762679456018 79688679715211433077020775266464514647091873261008328763257028189807736717 81454170250523018608495319068138257481070252817559459476987034665712738139 28620523475680821886070120361108315209350194743710910172696826286160626366 24350228409441914084246159360000000000000000000000000000000000000000000000 00000000000000000) without difficulty, but then taking the 256th root of that huge number (by raising it to the power of 1∕256) failed. It incorrectly produced the value ∞, whereupon n divided by that wrong result produced the zero. The point of failure seems to be around 170! or 10308, which looks suspiciously like an internal 64-bit floating-point representation limit.
Of course, we could work around that limitation, by changing the way we compute n-th roots. For example, the n-th root of a number also given by: 10log10X∕n
So we could try:
# n-th root of x...
sub infix:<√> (Int $n, Int $x --> Numeric) is tighter(&[**]) {
10 ** (log10($x) / $n)
}
...but we get exactly the same problem: the built-in log10 function breaks
at around 10308, meaning we can’t apply it to factorials of
numbers greater than 170.
But when X is an integer, there’s a surprisingly good approximation to log10X
that doesn’t have this 10308 limitation at all: we simply count the number of
digits in X and subtract ½.
In the worst cases, this result is out by no more than ±0.5, but that means its average
error over a sufficiently large range of values...is zero.
Using that approximation for n-th roots:
# n-th root of x...
sub infix:<√> (Int $n, Int $x --> Numeric) is tighter(&[**]) {
10 ** (($x.chars - ½) / $n)
}
...we can now extend our assessment of the de Moivre/Stirling approximation far beyond n=170. In which case we find:
[30] de Moivre/Stirling approximation (n = 1):
To our disgust, the convergence of this approach clearly does not accelerate at higher values of n.
In fact, even when n is over a million, the result is still only accurate to three decimal places; worse even than the classic palindromic fractional approximation:
#| Palindromic fraction
assess { 878
/ 323
}
...which gives us:
[40] Palindromic fraction:
Alas, the search continues.
𝑒 is for estimation
Let’s switch back to probability theory. Imagine a series of uniformly distributed random numbers in the range 0..1. For example:
0.162532, 0.682623, 0.4052625, 0.42167261, 0.99765261, ...
If we start adding those numbers up, how many terms of the series do we need to add
together before the total is greater than 1? In the above example, we’d need to add
the first three values to exceed 1. But in other random sequences we’d need to add only
two terms (e.g. 0.76217621, 0.55326178, ...) and occasionally we’d need to add quite
a few more (e.g. 0.1282827, 0.00262671, 0.39838722, 0.386272617, 0.77282873, ...).
Over a large number of trials, however, the average number of random values required
for the sum to exceed 1 is (you guessed it): 𝑒.
So, if we had a source of uniform random values in the range 0..1, we could get an
approximate value for 𝑒 by repeatedly adding sufficient random values to exceed 1,
and then averaging the number of values we required each time, over multiple trials.
Which looks like this in Raku:
#| Stochastic approximation
assess -> \trials=(10², 10³, 10⁴, 10⁵, 10⁶) {
sum( (1..trials).map:
{ ([\+] rand xx ∞).first(* > 1):k + 1 }
)
/ trials
}
That is: we conduct a specified number of trials (1..trials), and for each trial (.map:)
we generate an infinite number of uniform random values (rand xx ∞), which we then convert
to a list of progressive partial sums ([\+]). We then look for the first of these partial
sums that exceeds 1 (.first(* > 1)), find out its index in the list (:k) and add 1
(because indices start from zero, but counts start from 1).
The result is a list of counts of how many random values were required to exceed one in
each of our trials. As 𝑒 is the average of those counts, we sum them
and divide by the number of trials. And find:
[50] Stochastic approximation (trials = 100):
That’s pretty good...for random guessing. If we’d kept it running for a greater number of trials, we’d eventually have gotten reasonable accuracy. But it’s unreliable: sometimes losing accuracy as the number of trials increases. And it’s slow: only three digits of accuracy after a million trials...and 40 seconds of computation. To get a useful number of correct digits we’d need billions, possibly trillions, of trials...which would require tens, or thousands, of hours of computation.
So on we go....
𝑒 is for efficiency
Or, rather, back we go. Back to 1669, to that Isaac Newton of mathematical geniuses:
Isaac Newton. In a manuscript entitled
De analysi per aequationes numero terminorum infinitas
Newton set out a general approach to solving equations that are infinite series,
an approach that implies a highly efficient way of determining 𝑒.
Specifically, that: 𝑒 = Σ 1∕k! for k from 0 to ∞
So let’s try that:
#| Newton's series
assess -> \k=0..∞ { sum (0..k)»!»⁻¹ }
Here we compute 𝑒 by taking increasingly longer subsets of length k from the
infinite series of terms (\k=0..∞). We take the indices of the chosen terms
((0..k)), and for each
of them (») take its factorial (!). Then for each factorial
(») we take its reciprocal (⁻¹).
The result is a list of the successive terms
1∕k!, which we finally add together (sum) to get 𝑒:
[60] Newton's series (k = 0):
Finally...some real progress. After summing only 20 terms of the infinite 1∕k! series, we have 19 correct decimal places, and (at last!) a reasonably accurate value of 𝑒.
And we can do even better: 𝑒 can be decomposed into many other infinite summations.
For example: in 2003 Harlan Brothers
discovered
that 𝑒 = Σ (2k+1)∕(2k)!
which we could assess with:
#| Brothers series
assess -> \k=0..∞ {
sum (2 «×« (0..k) »+» 1) »/« (2 «×« (0..k))»!
}
By making every arithmetic operator a hyperoperator, we can compute the entire series of 0..k terms in a single vector expression and then sum them to get 𝑒.
The code for the Brothers formula might be a little uglier than for Newton’s original,
but it makes up for that by converging twice as fast, giving us 19 correct decimal places from
just the first ten terms in the series:
[70] Brothers series (k = 0):
𝑒 is for epsilon
We’re making solid progress on an accurate computation of 𝑒 with these two Newtonian series, but that ugly (and possibly scary) hyperoperated assessment code is still kinda irritating. And too easy to get wrong.
Given that these efficient methods all work the same way—by summing (an initial subset of) an infinite series of terms—maybe it would be better if we had a function to do that for us. And it would certainly be better if the function could work out by itself exactly how much of that initial subset of the series it actually needs to include in order to produce an accurate answer...rather than requiring us to manually comb through the results of multiple trials to discover that.
And, as so often in Raku, it’s surprisingly easy to build just what we need:
sub Σ (Unary $block --> Numeric) {
(0..∞).map($block).produce(&[+]).&converge
}
We call the subroutine Σ, because that’s the usual mathematical notation for this function
(okay, yes, and just because we can). We specify that it takes a one-argument block,
and returns a numeric value (Unary $block --> Numeric), with the return value representing a
“sufficiently accurate” summation of the series specified by the block.
To accomplish that, it first builds the infinite list of term indexes (0..∞) and passes
each in turn to the block (.map($block)). It then builds successive partial sums of the
resulting terms (.produce(&[+])). That is, if the block was { 1 / k! }, then the list
created by the .map would be: (1, 1, 1∕2, 1∕6, 1∕24, 1∕120, ...) and the .produce(&[+]) method call would progressively
add these, producing the list: 1, 1+1, 1+1+1∕2, 1+1+1∕2+1∕6, 1+1+1∕2+1∕6+1∕24, 1+1+1∕2+1∕6+1∕24+1∕120, ...)
That is: (1, 2, 2.5, 2.666, 2.708, 2.717, ...).
We set the calculation up this way because we need to be able to work out when to stop adding
terms, which will be when the successive elements of the .produce list converge
to a consistent value. In other words, when two successive values differ by only an
inconsequential amount.
And, conveniently, Raku has an operator that can tell us precisely that:
the ≅ is-approximately-equal-to operator (or
its ASCII equivalent: =~=).
So we could write a subroutine that takes a list and returns the first “converged” value
from it, like so:
sub converge(Iterable $list --> Numeric) {
$list.rotor(2=>-1).first({ .head ≅ .tail }).tail
}
The .rotor method extracts sublists of
N elements from its list. Here we tell it to extract two elements at a time, but to also make
them overlap, by stepping back one place (-1) between each extraction. The result is that,
from a list such as (1, 2, 2.5, 2.666, 2.708, 2.717 …), we get a list of lists of every
pair of adjacent values:
( (1, 2), (2, 2.5), (2.5, 2.667), (2.667, 2.708), (2.708, 2.717) …)
Then we simply step through the list of lists, looking for the first sublist in which the head and
tail elements are approximately equal (.first({ .head ≅ .tail })). That gives us back a single
sublist, from which we extract only the more-accurate tail element (.tail).
We can then just apply this function to the list of partial sums being produced in Σ:
(0..∞).map($block).produce(&[+]).&converge
...which is just a conveniently left-to-right way of passing the entire list into converge.
Of course, we could also have written it as a normal name-arglist style subroutine call:
converge (0..∞).map($block).produce(&[+])
...if that makes us more comfortable.
The insanely cool thing about all this—and the only reason it works at all—is that
every component of the two method-call chains within Σ and converge is lazily evaluated.
Which means that .map doesn’t actually execute the block on any of the (0..∞) values,
and .produce doesn’t progressively add any of them together, and .rotor doesn’t extract
any overlapping pairs of them, and .first doesn’t search any of them...unless the final
result requires them to. The .map only invokes the block as many times as necessary to
get enough values for .produce to add, to get enough values for .rotor to extract,
to get enough values for .first to find the first approximately equal pair.
I truly love that about Raku: not only does it allow you to write code that’s concise, expressive, and elegant; your concise, expressive, elegant code is naturally efficient as well.
Meanwhile, we now have a much better (i.e. more concise, more expressive, more elegant) way of generating a highly accurate value of 𝑒:
#| Newton's series
assess { Σ -> \k { 1 / k! } }
#| Brothers series
assess { Σ -> \k { (2×k + 1) / (2×k)! } }
...which give us the straightforward answers we were looking for:
[80] Newton's series:
[83] Brothers series:
𝑒 is for epigram
And that would be the end of the story...except that we’ve still ignored half of the
possibilities. Every technique we’ve tried so far has been mathematical in nature.
But Raku is not just for algebraists or statisticians or probability theorists.
It’s also for linguists and authors and poets and all other lovers of natural language.
So how could we use natural language to compute an accurate value of 𝑒?
Well, it turns out that algebraists and statisticians and probability theorists have been doing that for centuries. Because once you’ve spent several hours (or days, or weeks) manually calculating the first eight digits of 𝑒, you never want to have to do that again! So you come up with a mnemonic: a sentence that helps you remember those hard-won digits.
Most mnemonics of this kind work by encoding each digit in the length of successive words.
For example, to remember the constant 1.23456789, you might encode it as:
“I am the
only local Aussie abacist publicly available”. Then you just count the letters
of each
word to extract the digits.
As usual, that’s trivial to implement in Raku:
sub mnemonic(Str $text --> Str) {
with $text.words».trans(/<punct>+/ => '')».chars {
return "{.head}.{.tail(*-1).join}"
}
}
We first extract each word from the text ($text.words), and for each of them (»)
we remove any punctuation characters by translating them to empty strings
(.trans(/<punct>+/ => '')), and finally count the number of remaining
characters in each word (».chars). We then take the first element from that list
of
word lengths (.head), add a dot, and then append the concatenation of the rest
of the N-1 character counts (.tail(*-1).join), and return that as the
string representation of the resulting number.
Then we test it:
#| Mnemonic test
assess {
mnemonic "I am the only local Aussie abacist
publicly available"
}
...which prints:
[90] Mnemonic test:
...which is clearly a very poor approximation to 𝑒.
But for three centuries people have been making up better ones.
One of the most widely used is the slightly self-deprecating:
#| Modern mnemonic
assess {
mnemonic "It enables a numskull to remember
a sequence of numerals"
}
...which gives us nine correct decimal places:
[100] Modern mnemonic:
If we need more accuracy, we can just compose a longer sentence. For example:
#| Titular mnemonic
assess {
mnemonic "To compute a constant of calculus:
(A treatise on multiple ways)"
}
...which produces one additional digit:
[110] Titular mnemonic:
Or, for better accuracy than any of the mathematical approaches so far, we could use Zeev Barel’s self-referential description:
#| Extended mnemonic
assess {
mnemonic "We present a mnemonic to memorize a constant
so exciting that Euler exclaimed: '!'
when first it was found. Yes, loudly: '!'.
My students perhaps will compute e, via power
or Taylor series, an easy summation formula.
Obvious, clear, elegant!"
}
...which gives us far more accuracy than we’d ever actually need:
[120] Extended mnemonic:
𝑒 is for eclectic
And even that isn’t the end of the story. Just like π (its main rival for World’s Most Awesome Mathematical Constant), 𝑒 exerts a strange fascination over the mathematically whimsical.
For example, in 1988, Dario Castellanos
published the following identity:
𝑒 = (π4 + π5)1∕6
Which, translated to Raku is:
#| Castellano's coincidence
assess { (π⁴ + π⁵) ** ⅙ }
...and gives us seven decimal places of accuracy:
[130] Castellano's coincidence:
And those of us who can remember the digits 1 to 9 (or who know an Aussie abacist)
can use Richard Sabey’s formula: 𝑒 = (1 + 2-3×(4+5)).6×.7+89:
#| Sabey's digits
assess { (1+2**(-3×(4+5)))**(.6×.7+8⁹) }
...which (fittingly) gives us nine correct digits in total:
[140] Sabey's digits:
But those curiosities are as nothing compared to the true highlands of 𝑒 exploration.
For example, Maksymilian Piskorowski found that if you happen to have a spare
eight 9s, you can compute 𝑒 = (9∕9 + 9-99)999,
which is accurate to a little over 369 million
decimal places.
We could translate that easily enough to Raku:
#| Piskorowski's eight 9s
assess { (9/9 + 9**-9**9) ** 9**9**9 }
But, alas, our assessment fails (eventually), producing a disappointing:
[150] Piskorowski's eight 9s:
...because the value of 9-99 is so vanishingly small that adding it to
9∕9 in Raku
merely produces 1, and then 1999 is still 1.
Piskorowski’s incalculable ⅓ billion decimal places of accuracy seemed like the (il)logical end-point of this quest. But only until the aforesaid Richard Sabey spoiled the game for everyone, by reformulating his aforementioned pan-digital formulation to: 𝑒 = (1 + 9-47×6)3285
Which is accurate to a staggering 18457734525360901453873570 decimal places
(that’s 18.4 octillion digits)...but which, tragically, immediately underflows Raku’s
numeric representation when attempting to compute the initial 9-442;
Raku being unable to accurately represent 1∕919342813113834066795298816.
Meanwhile, if you’d like to further explore these and other 𝑒-related exotica,
check out Erich Friedman’s mesmerizing
Math Magic website.
𝑒 is for exquisite
There is still one higher mathematical summit for us to surmount in our quest
for 𝑒.
The pinnacle of mathematical elegance, the peak of arithmetical pulchritude,
the single most beautiful equation in all of mathematics:
Euler’s Identity
In 1748 Leonhard Euler published his masterwork:
Introductio in analysin infinitorum,
in which he included the first mention of the general
Euler Formula: 𝑒ix = cos x + i sin x.
Although not explicitly mentioned in the treatise, this formula implies a remarkable special
case (at x=π) of: 𝑒iπ = -1 + 0i
This special-case equality is nowadays more usually written: 𝑒iπ + 1 = 0
Thereby uniting the five most important constants in mathematics.
Quite apart from this extraordinarily lovely unification of mathematical fundamentals,
for our purposes the significant point here is that one of the five components is 𝑒.
And, if we rearrange the formula to isolate that constant, we get: 𝑒 = (-1)1∕πi
which we can easily assess in Raku:
#| From Euler's Identity
assess { (-1) ** (π×i)⁻¹ }
Unfortunately, Raku is not (yet) smart enough to infer from the imaginary exponent
that it needs to use the Complex version
of the ** operator
(well, yes, of course complex mathematics is already built into Raku).
So we get back:
[160] From Euler's Identity:
...because the non-complex exponentiation fails when given a complex exponent,
producing the value NaN+NaN\i.
But if we start with a suitably 2D version of -1 (i.e. -1+0i), like so:
#| From Euler's Identity
assess { (-1+0i) ** (π×i)⁻¹ }
...we get the correct complex arithmetic, and a highly accurate answer from it:
[160] From Euler's Identity:
𝑒 is for effortless
It’s fitting that we have now come full circle: finding Euler’s Number
from the special case of Euler’s Formula that is Euler’s Identity.
Euler’s Ouroboros, if you will.
All that effort...to end up more or less back where we started. Which is highly appropriate,
because where we started already had the answer built in. First of all, in the form of
the standard exp function, which returns the value of 𝑒x.
So we could have tried:
#| Built-in exp() function
assess -> \x=1 { exp(x) }
...which would have given us:
[170] Built-in exp() function (x = 1):
But even that is considerably more effort that we actually need in Raku.
Because (of course) the constant itself is also built right in to the language:
#| Built-in e constant
assess { e }
...and produces an equally accurate result:
[180] Built-in e constant:
So the optimal solution to the original task was just five characters long:
say e
...which shall henceforth be known as: “Euler’s One-liner”.
Damian