Perl Weekly Challenge 167: Circular Primes
These are some answers to the Week 167 of the Perl Weekly Challenge organized by Mohammad S. Anwar.
Spoiler Alert: This weekly challenge deadline is due in a few of days from now (on June 5, 2022 at 23:59). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.
Task 1: Circular Primes
Write a script to find out first 10 circular primes having at least 3 digits (base 10).
Please checkout wikipedia for more information.
A circular prime is a prime number with the property that the number generated at each intermediate step when cyclically permuting its (base 10) digits will also be prime.
Output:
113, 197, 199, 337, 1193, 3779, 11939, 19937, 193939, 199933
Given the task specification, I think that the suggested output is wrong. But I’ll come back to that later on.
Circular Primes in Raku
Raku has the built-in is-prime routine, which uses the fast Miller-Rabin test and makes the task quite easy. Fast as the is-prime routine may be, there is no reason loosing time running it on even numbers. So we start with a sequence generating odd numbers above 100. The rotate-and-test subroutine checks if rotations of the input number generate only prime numbers.
my $max = 10;
my $count = 0;
for 101, 103 ...* -> $n {
next unless $n.is-prime;
next unless rotate-and-test $n;
print "$n ";
$count++;
last if $count >= $max;
}
sub rotate-and-test ($i is copy) {
my $nb = $i.chars - 1;
for 0..^$nb {
$i = substr($i, 1) ~ substr($i, 0, 1);
return False unless $i.is-prime;
}
return True;
}
This program displays the following output:
$ raku ./circ-primes.raku
113 131 197 199 311 337 373 719 733 919
Note that my output here above is not the same as the example output provided with the task specification. But, clearly, 131 is a circular prime, since 113 is one (and 311 is also one). It appears that, in the output provided with the task specification, 131 and 311 are removed from the suggested solution because one item (113) of that cycle has already been displayed. But there is nothing in the task specification that tells us that it should be so. So, being a little bit stubborn, I won’t change my result. It would be easy to do so, though, as I will show in my Perl solution to the task below.
Circular Primes in Perl
Perl Circular Primes According to the Specification
Perl doesn’t have a built-in is_prime function, so we will implement our own subroutine. For this, we will test even division by prime numbers up to the square root of 919. Since we know from our Raku implementation that the largest number we need to test is 919, so that we need a list of primes up to 31. We will simply hard-code that list. The rest of the solution is essentially a port to Perl of the Raku program above.
use warnings;
use feature "say";
use constant MAX => 10;
my @primes = (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31); #Init small primes
sub is_prime {
my $n = shift;
for my $p (@primes) {
return 1 if $p >= $n;
return 0 if $n % $p == 0;
}
return 1;
}
sub rotate_and_test {
my $i = shift;
my $nb = length $i - 1;
for (1..$nb) {
$i = substr($i, 1) . substr($i, 0, 1);
return 0 unless is_prime $i;
$seen{$i} = 1;
}
return 1;
}
my $max = 10;
my $count = 0;
my $n = 99;
while (1) {
$n += 2;
next unless is_prime $n;
next if $seen{$n};
next unless rotate_and_test $n;
print "$n ";
$count++;
last if $count >= MAX;
}
This script displays the following output:
$ perl ./circ-primes.pl
113 131 197 199 311 337 373 719 733 919
Perl Circular Primes to Match the Suggested Solution
As noted before, my solution above is not the same as the solution suggested in the specification.
The reason for this difference is that the suggested solution is probably taken from the cited Wikipedia article, which does not provide a list of circular primes, but “the complete listing of the smallest representative prime from all known cycles of circular primes.”
In other words, this list removes 131 and 311 from the output, since 113 has already been displayed. It is not difficult to remove such numbers from the output, since we have already tried them. So, all we need to do is to store all tested numbers in a hash.
However, we will test primality of numbers much larger than before (up to about 1,000,000), so that we now need a list of primes up to about 1,000. We can no longer hard-code such a list of primes. So, we will use a smaller list of hard-coded primes, and add a loop to find all primes below 1,000.
use strict;
use warnings;
use feature "say";
use constant MAX => 10;
my %seen;
my @primes = (2, 3, 5, 7, 11); # Init small primes
my $i = $primes[-1];
LOOP: while (1) { # get primes until 1000
$i += 2;
last if $i > 1000;
my $sqrt = sqrt $i;
for my $p (@primes) {
last if $p >= $sqrt;
next LOOP if $i % $p == 0;
}
push @primes, $i;
}
sub is_prime {
my $n = shift;
for my $p (@primes) {
return 1 if $p >= $n;
return 0 if $n % $p == 0;
}
return 1;
}
sub rotate_and_test {
my $i = shift;
my $nb = length $i - 1;
for (1..$nb) {
$i = substr($i, 1) . substr($i, 0, 1);
return 0 unless is_prime $i;
$seen{$i} = 1;
}
return 1;
}
my $max = 10;
my $count = 0;
my $n = 99;
while (1) {
$n += 2;
next unless is_prime $n;
next if $seen{$n};
next unless rotate_and_test $n;
print "$n ";
$count++;
last if $count >= MAX;
}
This script displays the following output:
$ perl circ-primes.pl
113 197 199 337 1193 3779 11939 19937 193939 199933
We now have the same output as in the task specification, but, being as I said a little bit stubborn, I maintain that my original implementation was a better solution to the task specification.
Task 2: The Gamma Function
Implement subroutine gamma() using the Lanczos approximation method.
[2022-05-31] Ryan Thompson wrote an interesting blog explaining the subject in details. Highly recommended if you are looking for more information. BLOG.
Example:
print gamma(3); # 1.99
print gamma(5); # 24
print gamma(7); # 719.99
The information above about Ryan Thompson’s blog was not available yesterday when I wrote my Raku implementation below, but it is now when I’m writing this blog post.
The Gamma function is sort of an extension to real and complex numbers (except negative integers and zero) of the factorial function. Similarly to the factorial function, it satisfies the recursive relation:
f(1) = 1,
f(x + 1) = x f(x)
For integer input values, we have the following relation between the gamma function and the exponential function:
gamma(n) = (n - 1)!
which will be quite convenient to verify the results of our tests.
For those interested, this is what the Gamma function looks like:
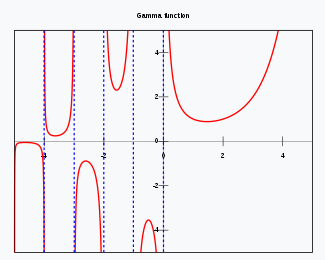
But the task is not so much about the gamma function, but more about the Lanczos approximation. I frankly couldn’t say anything about the Lanczos approximation that would not be plagiarized from the cited Wikipedia article (or possibly Ryan’s blog). So, the reader is kindly invited to check these sources.
The gamma Function in Raku
I don’t really understand the details in the Wikipedia article about the Lanczos approximation. So I decided to simply port to Raku the Python implementation provided in this article. This leads to the following Raku program:
use v6;
my @p = <676.5203681218851 -1259.1392167224028
771.32342877765313 -176.61502916214059
12.507343278686905 -0.13857109526572012
9.9843695780195716e-6 1.5056327351493116e-7>;
my constant EPSILON = 1e-07;
sub drop-imaginary(Complex $z) {
return $z.im.abs < EPSILON ?? $z.re !! $z;
}
sub gamma($z is copy) {
my $y;
if $z.re < 0.5 {
$y = pi / (sin(pi * $z) * gamma(1 - $z)); # reflection formula
} else {
$z -= 1;
my $x = 0.99999999999980993;
for @p.kv -> $i, $pval {
$x += $pval / ($z + $i +1);
}
my $t = $z + @p.elems - 0.5;
$y = sqrt(2 * pi) * $t ** ($z + 0.5) * (-$t).exp * $x;
}
return drop-imaginary $y;
}
for 1, 3, 5, 6.2, 7, 0.4 -> $i {
printf "$i -> %.5f\n", gamma $i.Complex;
}
This program displays the following output:
$ ./raku gamma.raku
1 -> 1.00000
3 -> 2.00000
5 -> 24.00000
6.2 -> 169.40610
7 -> 720.00000
0.4 -> 2.21816
As it can be seen, the relation:
gamma(n) = (n - 1)!
is satisfied for integer input values. For example, we have:
gamma(7) = 720 = 6!
It should be quite easy to port the same Python program to Perl, but I really won’t have time this week. I’m already quite happy that I was able to do it in Raku despite time constraints.
Wrapping up
The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on June 12, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.

 I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.
I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.