E. Choroba

I know I’m late with my blog post. I had the solutions ready in time, but I suffered a dental abscess and spent the rest of the week either praying for the painkillers to kick in or sleeping when they did.

Niven Numbers

A Niven number is a number divisible by the sum of its digits. To get the digits of a number, the easiest way is to split it. To sum them, I reached for List::Util and its sum(). Divisibility can be tested via the modulo operator %:

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

use List::Util qw{ sum };

say for grep 0 == $_ % sum(split //), 1 .. 50;

A Word Ladder

The basic idea is to start from the first word, find all the words that can be obtained from it by changing one of its letters, then getting new words obtainable from the first group, and so on until we find the target word or have no words to process. This technique is quite common and is usually called breadth-first search, because we always explore the nearest new words before going one step further.

Once the target word has been found, we need to process the groups backwards to find an actual ladder. We can’t construct it while creating the groups, because we don’t know yet which words will be part of the ladder.

To get the number of differing letter between two words, I used the XOR (^) operator. For two strings, it returns the character \0 for all the equal letters. To count the number of non-null characters, I used the tr operator in scalar context.

I used the American dictionary as it was a bit larger than the British one on my machine.

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

my $DICT = '/usr/share/dict/american';

main();

sub main {
    my @words = split ' ', <>;
    check_length(@words) or return;

    my $dict = load_dict(length $words[0]);
    check_existence($dict, @words) or return;
    my ($distance, $ladder) = bfs(@words[0, 1], $dict);
    say for $words[0], find_path($distance, $ladder, $words[1]);
}

sub check_length {
    my (@words) = @_;
    return @words == 2
           && length $words[0] == length $words[1]
           && $words[0] ne $words[1]
}

sub check_existence {
    my ($dict, @words) = @_;
    return 2 == grep exists $dict->{$_}, @words
}

sub is_close {
    my ($w1, $w2) = @_;
    my $diff = $w1 ^ $w2;
    return 1 == $diff =~ tr/\0//c
}

sub load_dict {
    my ($length) = @_;

    my %dict;
    open my $in, '<', $DICT or die $!;
    while (<$in>) {
        chomp;
        undef $dict{$_} if $length == length && /^[a-z]+$/;
    }
    return \%dict
}

sub bfs {
    my ($start, $final, $dict) = @_;
    my $distance = 0;
    my %agenda = ($start => undef);
    my %accessible;
    while (keys %agenda) {
        my %next;
        for my $n (keys %agenda) {
            for my $word (keys %$dict) {
                if (is_close($word, $n) && ! exists $accessible{$word}) {
                    $accessible{$word} = $distance + 1;
                    return $distance, \%accessible if $word eq $final;

                    undef $next{$word};
                }
            }
        }
        %agenda = %next;
        ++$distance;
        # say $distance, ' ', scalar keys %agenda;
    }
    return
}

sub find_path {
    my ($distance, $ladder, $final) = @_;

    my @ladder = my $previous = $final;
    while ($distance) {
        $previous = (grep $ladder->{$_} == $distance && is_close($previous, $_),
                          keys %$ladder)[0];
        --$distance;
        unshift @ladder, $previous;
    }
    return @ladder
}

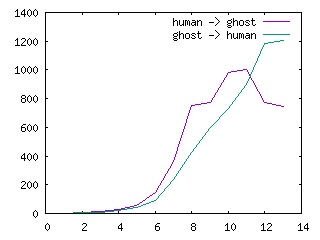
If you uncomment the line near the bottom of the bfs() subroutine, you’ll see the number of potential words in each step. It can get pretty large for longer words; for example, this is how to get from human to ghost in 14 steps:

1 2
2 9
3 12
4 26
5 54
6 147
7 361
8 750
9 773
10 981
11 1001
12 775
13 747
human
humas
humus
mumus
mumms
mummy
gummy
gammy
gaumy
gaums
glums
gloms
gloss
glost
ghost

Interestingly, going the other way round doesn’t show the same pattern, the number of words is always increasing. There are more words similar to human than to ghost.

1 2
2 5
3 10
4 23
5 45
6 94
7 240
8 424
9 597
10 732
11 898
12 1181
13 1204