E. Choroba

Write a script that takes 2 or more strings as command line parameters and prints the longest common substring.

A naive solution

For a naive solution, we first need to make an observation: although the longest common substring (lcs) must be a substring of all the strings, we don’t have to process all pairs of strings to find it. We can just take all the substrings of one of the strings (using the shortest one would be fastest) and try to find each substring in all other strings. If the substring is present in all the strings and is longer than the lcs found so far, we have a new lcs candidate. I decided to keep all the lcs’s of the same length.

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

my @longest = ("");
my $string  = shift;
for my $pos (1 .. length $string) {
    for my $length (1 .. 1 - $pos + length $string) {
        next if $length < length $longest[0];

        my $substr = substr $string, $pos - 1, $length;
        my $found = 0;
        -1 != index $_, $substr and ++$found for @ARGV;
        if ($found == @ARGV) {
            if ($length == length $longest[0]) {
                push @longest, $substr;
            } else {
                @longest = $substr;
            }
        }
    }
}
say "<$_>" for @longest;

Using next is another optimisation: there’s no need to try a substring that’s shorter than the lcs found so far.

The algorithm seems to work fine for simple inputs, but when I tried to run it on two 10KB sized text documents, it took it more than 1m 30s to finish. That was expected and I wanted to find a more effective solution.

Suffix trees

The linked Wikipedia page mentions a generalised suffix tree as the data structure to use for a linear time solution. It can be built using Ukkonen’s algorithm which I saw mentioned before when studying bioinformatics. In fact, I’ve tried several times to implement it, but the original paper is rather long and as I’ve never needed the algorithm for work, I’ve always given up. But not this time.

The last mentioned page contains a link that either didn’t exist last time I checked it, or maybe I just overlooked it. It points to a Stack Overflow question that asks about the algorithm, and one of the answers explains the algorithm “in plain English”. Moreover, there are several links to implementations in various languages, so I didn’t have to start from scratch. In the end, I found Sergey Makagonov’s Java solution short and easy to follow and decided to build my Perl solution on it.

Direct translation of the Java implementation is here:

#!/usr/bin/perl
use warnings;
use strict;

{   package My::Node;
    sub new { bless { start => $_[1], end => $_[2] }, $_[0] }
    sub edge_length {
        my ($self, $position) = @_;
        ($self->{end} < $position + 1
            ? $self->{end}
            : $position + 1
        ) - $self->{start}
    }
}
{   package My::Suffix::Tree;

    sub new {
        my ($class) = @_;
        bless my $self = {position      => -1,
                          text          => "",
                          active_edge   => 0,
                          active_length => 0,
                          current_node  => -1,
        }, $class;
        $self->{root} = $self->new_node(-1, -1);
        $self->{active_node} = $self->{root};
        return $self
    }

    sub add_word {
        my ($self, $word) = @_;
        $self->add_char($_) for split //, $word;
    }

    sub _add_suffix_link {
        my ($self, $node) = @_;
        $self->{nodes}[ $self->{need_suffix_link} ]{link} = $node
            if $self->{need_suffix_link} > 0;
        $self->{need_suffix_link} = $node;
    }

    sub active_edge { substr $_[0]{text}, $_[0]{active_edge}, 1 }

    sub walk_down {
        my ($self, $next) = @_;
        $next //= 0;
        my $position = $self->{position};
        if ($self->{active_length}
            >= $self->{nodes}[$next]->edge_length($position)
        ) {
            $self->{active_edge}
                += $self->{nodes}[$next]->edge_length($position);
            $self->{active_length}
                -= $self->{nodes}[$next]->edge_length($position);
            $self->{active_node} = $next;
            return 1
        }
        return
    }

    sub new_node {
        my ($self, $start, $end) = @_;
        $self->{nodes}[ ++$self->{current_node} ]
            = 'My::Node'->new($start, $end);
        $self->{current_node}
    }

    sub add_char {
        my ($self, $char) = @_;
        substr $self->{text}, ++$self->{position}, 1, $char;
        $self->{need_suffix_link} = -1;
        ++$self->{remainder};
        while ($self->{remainder} > 0) {
            $self->{active_edge} = $self->{position}
                unless $self->{active_length};
            if (! exists
                $self->{nodes}[ $self->{active_node} ]
                    {next}{ $self->active_edge }
            ) {
                $self->{nodes}[ $self->{active_node} ]
                    {next}{ $self->active_edge }
                    = $self->new_node($self->{position}, 'INF');
                $self->_add_suffix_link($self->{active_node});  # Rule 2.
            } else {
                my $next = $self->{nodes}[ $self->{active_node} ]
                    {next}{ $self->active_edge };
                next if $self->walk_down($next);  # Observation 2.

                # Observation 1.
                if ($char eq substr $self->{text},
                        $self->{nodes}[$next]{start} + $self->{active_length}, 1
                ) {
                    ++$self->{active_length};
                    # Observation 3.
                    $self->_add_suffix_link($self->{active_node});
                    last
                }
                my $split = $self->new_node($self->{nodes}[$next]{start},
                    $self->{nodes}[$next]{start} + $self->{active_length});
                $self->{nodes}[ $self->{active_node} ]{next}
                    { $self->active_edge } = $split;
                my $leaf = $self->new_node($self->{position}, 'INF');
                $self->{nodes}[$split]{next}{$char} = $leaf;
                $self->{nodes}[$next]{start} += $self->{active_length};
                $self->{nodes}[$split]{next}{ substr $self->{text},
                    $self->{nodes}[$next]{start}, 1 } = $next;
                $self->_add_suffix_link($split);  # Rule 2.
            }
            -- $self->{remainder};

            if ($self->{active_node} == $self->{root}
                && $self->{active_length} > 0  # Rule 1.
            ) {
                --$self->{active_length};
                $self->{active_edge}
                    = $self->{position} - $self->{remainder} + 1;
            } else {
                $self->{nodes}[ $self->{active_node} ]{link} //= 0;
                $self->{active_node}
                    = $self->{nodes}[ $self->{active_node} ]{link} > 0
                    ? $self->{nodes}[ $self->{active_node} ]{link}
                    : $self->{root};  # Rule 3.
            }
        }
    }
}

my $o = 'My::Suffix::Tree'->new;
$o->add_word(shift);

Unfortunately, we can’t use the code directly to solve our problem: it only builds a suffix tree for one string, not several strings. Fortunately, building a generalised suffix tree for several strings can be simulated by a simple suffix tree by just concatenating the input strings, using special marks as separators. I used <0>, <1> etc. as the markers.

Once we have the generalised suffix tree, we need to find a node that covers the final marks of all the input strings. The path corresponding to such a node represents a common substring, we just need to find the longest one(s). For example, let’s build the tree for the pair of strings ABAB and BABA, or for the string ABAB<0>BABA<1>.

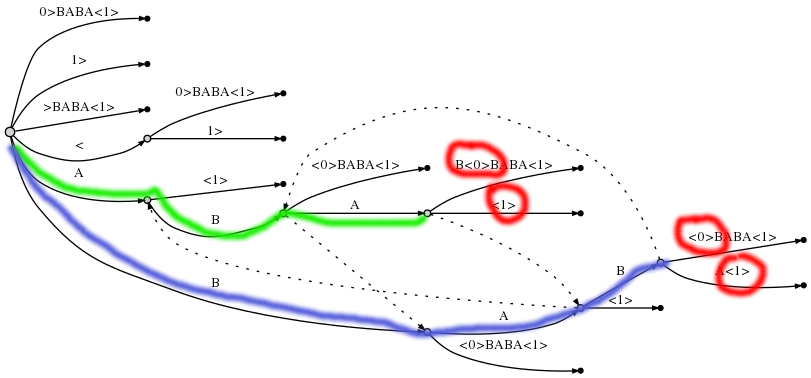
The two paths corresponding to the lcs’s ABA and BAB are highlighted in green and blue; the red circles help us verify that the final nodes of the paths cover both the marks <0> and <1>.

To accept a list of strings instead of a single string, we can delete the add_word method, introducing add_words instead:

    sub add_words {
        my ($self, @words) = @_;
        $self->{number_of_words} = @ARGV;
        for my $word_index (0 .. $#words) {
            $self->add_char($_)
                for split //, "$words[$word_index]<$word_index>";
        }
        my $text_length = length $self->{text};
        for my $node (@{ $self->{nodes} }) {
            next if $node->{start} < 0;
            my $text = $node->{end} > $text_length
                     ? substr $self->{text}, $node->{start}
                     : substr $self->{text}, $node->{start},
                           $node->{end} - $node->{start};
            $node->{text} = $text;
            if (my ($number) =  $text =~ /<([0-9]+)>/) {
                $node->{number} = $number;
            }
        }
        $self->add_numbers(0);
    }

The $node->{text} caches the substring corresponding to each node of the tree, $node->{number} corresponds to the first input marker covered by a leaf node (do you remember the red circles?).

We can also recursively propagate the covered marks to inner nodes of the tree. I cached the covered marks in $node->{numbers}. This method gets called after all the words have been added:

    sub add_numbers {
        my ($self, $node_index) = @_;
        my $node = $self->{nodes}[$node_index];
        for my $next_index (values %{ $node->{next} }) {
            undef $node->{numbers}{$_} for $self->add_numbers($next_index);
        }
        return $node->{number} // () unless exists $node->{numbers};

        return keys %{ $self->{numbers} }
    }

We now have all the information we need to find the lcs’s.

    my @lcs;
    sub longest_common_substring {
        my ($self, $node_index, $string) = @_;
        @lcs = ("") unless $node_index;
        my $node = $self->{nodes}[$node_index];

        if ($self->{number_of_words} == keys %{ $node->{numbers} }) {
            my $compare_lengths = length $string <=> length $lcs[0];
            push @lcs, $string if $compare_lengths == 0;
            @lcs = ($string) if $compare_lengths == 1;
        }

        for my $next_char (keys %{ $node->{next} }) {
            my $next_index = $node->{next}{$next_char};
            my $next = $self->{nodes}[$next_index];
            $self->longest_common_substring(
                $next_index,
                "$string$next->{text}");
        }
        return @lcs
    }

The condition $self->{number_of_words} == keys %{ $node->{numbers} } means "the node covers all the marks”.

To actually run the program, we need to initialise the object and run the search:

my $o = 'My::Suffix::Tree'->new;
$o->add_words(@ARGV);
say "<$_>" for $o->longest_common_substring(0, "");

The speed-up for the 10KB documents was immense. Instead of 1m 30s, the program now finishes in 0.45s, still giving the same results!

Conclusion

I’ve spent several nights on this. Why? I knew there was a Tree::Suffix, but its documentation says

NOTICE: as libstree has outstanding bugs and has long been abandoned, this distribution is not being maintained.

There was also SuffixTree, but it didn’t provide all the methods needed to implement the lcs search.

What about the other task?

You might have noticed I didn’t mention the second task, implementing a priority queue. You can read about my solution in the next blog post. Each theme is complex enough to deserve a separate blog post.