laurent_r

These are some answers for Week 133 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on October 10, 2021 at 23:59). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Integer Square Root

You are given a positive integer $N.

Write a script to calculate the integer square root of the given number.

Please avoid using built-in function. Find out more about it https://en.wikipedia.org/wiki/Integer_square_root.

Examples:

Input: $N = 10
Output: 3

Input: $N = 27
Output: 5

Input: $N = 85
Output: 9

Input: $N = 101
Output: 10

The standard method for calculating the square root of a number is the Newton method, a.k.a. Newton-Raphson method. For an integer square root, we may use a variation of that method called Heron’s method.

Integer Square Root in Raku

Using a Bisection Method

Before we implement the fairly fast standard method, let’s see what we can do with a bisection method, which is similar to a binary search algorithm on a list of values. If the input number is $N, then we look at the 1..$N interval and find the midpoint $est as the first estimate of the square root. If the square of the midpoint is larger than $N, then we continue with the 1..$est interval, else we continue with the $est..$N interval. We continue until the range is smaller than or equal to 1.

This is an implementation of this idea:

use v6;

sub sqroot (Int $a) {
    # Bisection approach
    my $start = 1;
    my $end = $a;
    my $est;
    loop {
        $est = ($start + $end) div 2;
        say "\tIntermediate values: $start, $est, and $end";
        my $est-sq = $est ** 2;
        last if abs($end-$start) <= 1;
        if $est ** 2 > $a {
            $end = $est;
        } else {
            $start = $est;
        }
    }
    return $est;
}
say "$_\t", sqroot $_ for 10, 27, 85, 101, 200_000_000;

This program displays the following output:

$ raku ./int_sqrt_bs.raku
    Intermediate values: 1, 5, and 10
    Intermediate values: 1, 3, and 5
    Intermediate values: 3, 4, and 5
    Intermediate values: 3, 3, and 4
10  3
    Intermediate values: 1, 14, and 27
    Intermediate values: 1, 7, and 14
    Intermediate values: 1, 4, and 7
    Intermediate values: 4, 5, and 7
    Intermediate values: 5, 6, and 7
    Intermediate values: 5, 5, and 6
27  5
    Intermediate values: 1, 43, and 85
    Intermediate values: 1, 22, and 43
    Intermediate values: 1, 11, and 22
    Intermediate values: 1, 6, and 11
    Intermediate values: 6, 8, and 11
    Intermediate values: 8, 9, and 11
    Intermediate values: 9, 10, and 11
    Intermediate values: 9, 9, and 10
85  9
    Intermediate values: 1, 51, and 101
    Intermediate values: 1, 26, and 51
    Intermediate values: 1, 13, and 26
    Intermediate values: 1, 7, and 13
    Intermediate values: 7, 10, and 13
    Intermediate values: 10, 11, and 13
    Intermediate values: 10, 10, and 11
101 10
    Intermediate values: 1, 100000000, and 200000000
    Intermediate values: 1, 50000000, and 100000000
    Intermediate values: 1, 25000000, and 50000000
    Intermediate values: 1, 12500000, and 25000000
    Intermediate values: 1, 6250000, and 12500000
    Intermediate values: 1, 3125000, and 6250000
    Intermediate values: 1, 1562500, and 3125000
    Intermediate values: 1, 781250, and 1562500
    Intermediate values: 1, 390625, and 781250
    Intermediate values: 1, 195313, and 390625
    Intermediate values: 1, 97657, and 195313
    Intermediate values: 1, 48829, and 97657
    Intermediate values: 1, 24415, and 48829
    Intermediate values: 1, 12208, and 24415
    Intermediate values: 12208, 18311, and 24415
    Intermediate values: 12208, 15259, and 18311
    Intermediate values: 12208, 13733, and 15259
    Intermediate values: 13733, 14496, and 15259
    Intermediate values: 13733, 14114, and 14496
    Intermediate values: 14114, 14305, and 14496
    Intermediate values: 14114, 14209, and 14305
    Intermediate values: 14114, 14161, and 14209
    Intermediate values: 14114, 14137, and 14161
    Intermediate values: 14137, 14149, and 14161
    Intermediate values: 14137, 14143, and 14149
    Intermediate values: 14137, 14140, and 14143
    Intermediate values: 14140, 14141, and 14143
    Intermediate values: 14141, 14142, and 14143
    Intermediate values: 14142, 14142, and 14143
200000000   14142

This works well, but isn’t very efficient because our first estimates of the square root are quite far away from the actual root. We can improve the process significantly by starting the process with an estimate which is much closer to the target. For example, we can use 2 ** (((log2 N)/2).Int + 1), which is the least power of 2 larger than the square root of N, as our first estimate. This improved version may look like this:

sub sqroot (Int $a) {
    # Bisection approach
    my $start = 1;
    my $end = $a;
    my $est = 2 ** (((log2 $a)/2).Int + 1);
    loop {
        say "\tIntermediate values: $start, $est, and $end";
        last if abs($end-$start) <= 1;
        if $est ** 2 > $a {
            $end = $est;
        } else {
            $start = $est;
        }
        $est = ($end + $start) div 2;
    }
    return $est;
}
say "$_\t", sqroot $_ for 85, 101, 200_000_000;

This improved version displays the following output:

$ raku ./int_sqrt_bs2.raku
    Intermediate values: 1, 16, and 85
    Intermediate values: 1, 8, and 16
    Intermediate values: 8, 12, and 16
    Intermediate values: 8, 10, and 12
    Intermediate values: 8, 9, and 10
    Intermediate values: 9, 9, and 10
85  9
    Intermediate values: 1, 16, and 101
    Intermediate values: 1, 8, and 16
    Intermediate values: 8, 12, and 16
    Intermediate values: 8, 10, and 12
    Intermediate values: 10, 11, and 12
    Intermediate values: 10, 10, and 11
101 10
    Intermediate values: 1, 16384, and 200000000
    Intermediate values: 1, 8192, and 16384
    Intermediate values: 8192, 12288, and 16384
    Intermediate values: 12288, 14336, and 16384
    Intermediate values: 12288, 13312, and 14336
    Intermediate values: 13312, 13824, and 14336
    Intermediate values: 13824, 14080, and 14336
    Intermediate values: 14080, 14208, and 14336
    Intermediate values: 14080, 14144, and 14208
    Intermediate values: 14080, 14112, and 14144
    Intermediate values: 14112, 14128, and 14144
    Intermediate values: 14128, 14136, and 14144
    Intermediate values: 14136, 14140, and 14144
    Intermediate values: 14140, 14142, and 14144
    Intermediate values: 14142, 14143, and 14144
    Intermediate values: 14142, 14142, and 14143
200000000   14142

Using Heron’s Method

This method looks iteratively for a solution to the x² - N = 0 equation. With Newton’s method which applies to general numbers (not only integers), if you start with almost any estimate, p, you can compute a better estimate q with the following formula: q = (p + a / x) / 2. Geometrically, this is like drawing a tangent to the curve at the point where the abscissa is the first estimate, and take the point where the tangent meets the x axis as the new estimate. As it can be seen, we quickly get closer to the searched value (the square root), which is where the curve intersects the x-axis.

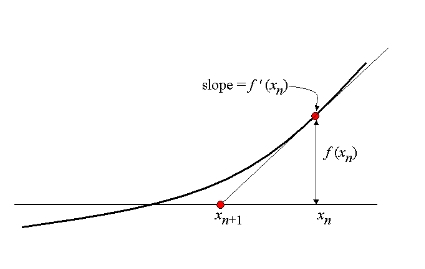
For integer square roots, we essentially need to replace standard rational division by Euclidean division (or integer division).

We use again 2 ** (((log2 N)/2).Int + 1) as our first estimate (see above).

use v6;

sub sqroot (Int $a) {
    my $x = 2 ** (((log2 $a)/2).Int + 1);
    my $y;
    loop {
        say "\tIntermediate value: $x";
        $y = ($x + $a div $x) div 2;
        last if abs($x - $y) < 1;
        $x = $y;
    }
    return $y;
}
say "$_\t", sqroot $_ for 10, 27, 85, 101, 200_000_000;

This program displays the following output:

$ raku ./int_sqrt.raku
    Intermediate value: 4
    Intermediate value: 3
10  3
    Intermediate value: 8
    Intermediate value: 5
27  5
    Intermediate value: 16
    Intermediate value: 10
    Intermediate value: 9
85  9
    Intermediate value: 16
    Intermediate value: 11
    Intermediate value: 10
101 10
    Intermediate value: 16384
    Intermediate value: 14295
    Intermediate value: 14142
200000000   14142

As it can be seen, this method converges toward the root much faster than the bisection method.

Integer Square Root in Perl

Using a Bisection Method

We again start with a bisection method. Please refer to the Bisection Method sub-section in the Raku section above for further explanations.

Perl doesn’t have a div Euclidean division operator, but it is easy to replace it with a combination of the standard division operator / and the int built-in function. Similarly, there is no built-in log2 binary logarithm function in Perl, but we can easily do without it, since we have the following mathematical property: log2 x = log x / log 2 (where log is the logarithm in any base, including the natural or the decimal logarithm).

use strict;
use warnings;
use feature "say";

sub sqroot {
    # Bisection method
    my $c = shift;
    my $start = 1;
    my $end = $c;
    my $est = 2 ** (int((log($c)/log(2))/2) + 1);
    while (1) {
        say "\tIntermediate values: $start, $est, and $end";
        last if abs($end-$start) <= 1;
        if ($est ** 2 > $c) {
            $end = $est;
        } else {
            $start = $est;
        }
        $est = int (($end + $start) / 2);
    }
    return $est;
}
say "$_\t", sqroot $_ for 85, 101, 200_000_000;

This script displays the same output as the equivalent Raku script above, so, for brevity, we only show the beginning of the output:

$ perl int_sqrt_BS.pl
        Intermediate values: 1, 16, and 85
        Intermediate values: 1, 8, and 16
        Intermediate values: 8, 12, and 16
        Intermediate values: 8, 10, and 12
        Intermediate values: 8, 9, and 10
        Intermediate values: 9, 9, and 10
85      9
        Intermediate values: 1, 16, and 101
        Intermediate values: 1, 8, and 16
        Intermediate values: 8, 12, and 16
        Intermediate values: 8, 10, and 12
        Intermediate values: 10, 11, and 12
        Intermediate values: 10, 10, and 11
101     10
...

Using Heron’s Method

This is essentially a port to Perl of the Raku program above (please look there for further explanations):

use strict;
use warnings;
use feature "say";

sub sqroot {
    my $c = shift;  # my $x = 2 ** (int((log($c)/log(2))/2) + 1);
    my $x = 2 ** (int((log($c)/log(2))/2) + 1);
    my $y;
    while (1) {
        say "\tIntermediate value: $x";
        $y = int(($x + $c / $x) / 2);
        last if abs($x - $y) < 1;
        $x = $y;
    }
    return $y;
}
say "$_ -> ", sqroot $_ for 10, 27, 85, 101, 200_000_000;

Output:

$ perl int_sqrt.pl
        Intermediate value: 2
        Intermediate value: 3
10 -> 3
        Intermediate value: 4
        Intermediate value: 5
27 -> 5
        Intermediate value: 8
        Intermediate value: 9
85 -> 9
        Intermediate value: 8
        Intermediate value: 10
101 -> 10
        Intermediate value: 8192
        Intermediate value: 16303
        Intermediate value: 14285
        Intermediate value: 14142
200000000 -> 14142

Task 2: Smith Numbers

Write a script to generate first 10 Smith Numbers in base 10.

According to https://en.wikipedia.org/wiki/Smith_number, in number theory, a Smith number is a composite number for which, in a given number base, the sum of its digits is equal to the sum of the digits in its prime factorization in the given number base.

Smith Numbers in Raku

For this task, we use a prime-factors subroutine that performs a prime factorization of the input parameter. We then iterates over successive integers (except those that are prime) and push the integer on a @result array if the sum of its digits is equal to the sum of the digits of its prime factors

use v6;

my @primes = grep {.is-prime}, 1..*;

sub prime-factors (UInt $num-in) {
    my @factors;
    my $num = $num-in;
    for @primes -> $div {
        while ($num %% $div) {
            push @factors, $div;
            $num div= $div;
        }
        return @factors if $num == 1;
    }
    push @factors, $num unless $num == $num-in;
    return @factors;
}

my @result;
my $count = 0;
for 1..* -> $i {
    next if $i.is-prime; # we want composite numbers only
    my @factors = prime-factors $i;
    push @result, $i and ++$count if (|@factors).comb.sum == $i.comb.sum;
    last if $count >= 10;
}
say @result;

This program displays the following output:

$ raku ./smith_nums.raku
[4 22 27 58 85 94 121 166 202 265]

Smith Numbers in Perl

This is essentially the same algorithm as in Raku, except that we have to build our own prime-factors and add_digits subroutines and implement a loop to populate the @primes array.

#!/usr/bin/perl
use strict;
use warnings;
use feature qw/say/;
use Data::Dumper;
use constant MAX => 400;

my @primes = (2, 3, 5, 7);
my $current = 9;
while (1) {
    my $prime = 1;
    for my $i (@primes) {
        my $i_sq = $i * $i;
        last if $i_sq > $current;
        $prime = 0, last if $current % $i == 0;  
    }
    push @primes, $current if $prime;;
    $current += 2;
    last if $current > MAX;
}
my %primes = map { $_ => 1} @primes;

sub prime_factors {
    my $num = shift;
    my $origin_num = $num;
    my @factors;
    for my $div (@primes) {
        while ($num % $div == 0) {
            push @factors, $div;
            $num /= $div;
        }
        return @factors if $num == 1;
    }
    push @factors, $num unless $num == $origin_num;
    return @factors;
}

sub add_digits {
my $sum = 0;
    for my $i (@_) {
        $sum += $_ for split //, $i;
    }
    return $sum;
}
# say join " ", prime_factors $_ for grep {not exists $primes{$_}} 2..50;

my @result;
my $count = 0;
my $i = 2;
while (1) {
    $i++;
    next if exists $primes{$i}; # we want composite numbers only
    my @factors = prime_factors $i;
    push @result, $i and $count++ if add_digits($i) == add_digits(@factors);
    last if $count >= 10;
}
say "@result";

The program displays the following output:

$ perl ./smith_nums.pl 4 22 27 58 85 94 121 166 202 265

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on October 17, 2021. And, please, also spread the word about the Perl Weekly Challenge if you can.