These are some answers to the Week 146 of the Perl Weekly Challenge organized by Mohammad S. Anwar.
Spoiler Alert: This weekly challenge deadline is due in a few days from now (on January 9, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.
Task 1: 10001st Prime Number
Write a script to generate the 10001st prime number.
10001st Prime Number in Raku
Raku has a fast is-prime subroutine or method, using the Miller-Rabin algorithm, to test whether a integer is prime. We can just generate an infinite (lazy) list of prime numbers and look for the 10000st one.
use v6;
my @primes = grep { .is-prime }, (1, 2, 3, -> $a { $a + 2} ...Inf);
say @primes[10001 - 1]; # Subtract 1 because the array starts at 0
This script displays the following output:
$ raku ./10001prime.raku
104743
The Raku script is so simple that it can be implemented as a short Raku one-liner:
$ ./raku -e 'say (grep { .is-prime }, 1..Inf)[10000]'
104743
10001st Prime Number in Perl
Since Perl doesn’t have a built-in is-prime subroutine, we implement our own. As finding the first 10001 primes is an intensive computation, we implement three performance optimizations compared to the naive brute-force solution: first, with the exception of 2, we only check odd integers. Second, we limit the tested divisors to the square root of the integer being checked. Finally, rather than testing all possible divisors, we test only the primes that we have already found. With these three optimizations, the script runs in less than 0.2 second, much faster than I expected.
use strict;
use warnings;
use feature "say";
use constant MAX => 10_001;
sub primes {
my $max = shift;
my @primes = (2, 3, 5);
my $count = 3;
my $candidate = $primes[-1];
while ($count <= $max) {
$candidate += 2;
my $not_prime = 0;
my $sq_cand = sqrt $candidate;
for my $i (@primes) {
$not_prime = 1, last unless $candidate % $i;
last if $i > $sq_cand;
}
next if $not_prime;
push @primes, $candidate;
$count ++;
}
return $primes[$max-1];
}
my $p = primes(MAX);
say "$p";
This script displays the following output:
$ time perl ./10001prime.pl
104743
real 0m0,192s
user 0m0,124s
sys 0m0,077s
10001st Prime Number in Ring
I continue my exploration of Ring, a recent programming language (the first version was issued in 2016). The Ring implementation below is essentially a port of the Perl program above (with same performance optimizations):
p = primes(10001)
see p + nl
func primes max
primes = [2, 3, 5]
count = len(primes)
candidate = primes[count]
while count < max
candidate += 2
is_prime = True
sqrt_cand = sqrt(candidate)
for i in primes
if candidate % i = 0
is_prime = False
exit
ok
if i > sqrt_cand exit ok
next
if is_prime
add(primes, candidate)
count ++
ok
end
return primes[max]
This program displays the following output:
$ ring ./10001prime.ring
104743
Note that Ring lists start with subscript 1, so we use index 10001 for finding the 10001 ptime number.
10001st Prime Number in Julia
function getprimes(max)
primes = [2, 3, 5]
count = 3
candidate = 5
while (count <= max)
candidate += 2
not_prime = false
sq_cand = sqrt(candidate)
for i in primes
if (candidate % i == 0)
not_prime = true
break
end
i > max && break
end
not_prime && continue
push!(primes, candidate)
count += 1
end
return primes[max] # Julia arrays start with index 1
end
p = getprimes(10001)
println(p)
This program displays the following output:
$ julia 10001prime.jl
104743
Task 2: Curious Fraction Tree
Consider the following Curious Fraction Tree:
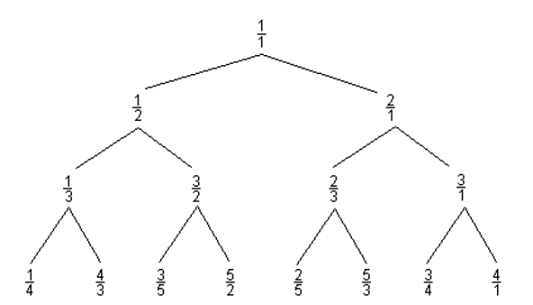
You are given a fraction, member of the tree created similar to the above sample.
Write a script to find out the parent and grandparent of the given member.
Example 1:
Input: $member = '3/5';
Output: parent = '3/2' and grandparent = '1/2'
Example 2:
Input: $member = '4/3';
Output: parent = '1/3' and grandparent = '1/2'
The first problem is to understand how this tree is constructed.
Each fraction has two children. It is easy to see that the left child is always a number smaller than 1 and the right child is always a number larger than 1. But how are the values generated?
Well, it is probably not so difficult to find out, but I must confess that I did not try very hard to find the constructing rules, but found them on the Curious Fraction Tree Web page. They are explained in this diagram:
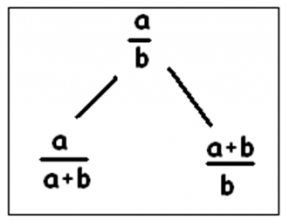
In other words, we have the following rules:
- For any node, the left child is less than 1 et the right child larger than 1;
- For node
a/b, left child is a/(a+b) and right node is (a+b)/b.
From these two rules, it is easy to derive the reciprocal rules for finding the parent of a node:
- For a node
x/y with a fraction less than 1, the parent is x/(y-x);
- For a node
x/y with a fraction larger than 1, the parent is (x-y)/x.
It is now very easy to implement these rules in various programming languages.
There is, however, one little last problem. The task specifications do not tell us what to do about invalid input. For example, if the input is (1, 1) (the root to the tree), we will not be able to find a parent. Similarly, if we are given (1/2) as input, we will find (1, 1) as the parent, and will not be able to the grand-parent. We would have a problem if one of the values is 0. It is fairly easy to detect these problems, but I still wouldn’t know what to do about it. In many of the implementations below, I have decided that we must be given a valid input and will not try to validate the input. In some others, I have decided to detect some of these invalid input problems and tried to do something reasonable about them.
Curious Fraction Tree in Raku
We’re just implementing the rules above. Here, I do not try to validate the input.
Note that I was first tempted to implement the fraction as a Rat type of value, since it implements it as a numerator/denominator pair. I finally decided not to do that (because there may be some cases where the fraction might be reduced to their simplest form, division by 0 errors, and other such problems). So I decided to implement the fractions as integer pairs.
use v6;
# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x
sub parent (\num, \denom) {
return num < denom ?? (num, denom - num) !! (num - denom, denom);
}
for (5, 2), (2, 5), (3, 4), (3, 5) -> $fraction {
my $parent = parent |$fraction[0,1];
my $gd-parent = parent |$parent[0,1];
say "for child $fraction, parent is $parent and gd-parent is $gd-parent";
}
With the test fractions provided in the code, this program displays the following output:
raku ./fraction-tree.raku
for child 5 2, parent is 3 2 and gd-parent is 1 2
for child 2 5, parent is 2 3 and gd-parent is 2 1
for child 3 4, parent is 3 1 and gd-parent is 2 1
for child 3 5, parent is 3 2 and gd-parent is 1 2
Curious Fraction Tree in Perl
This program implements the rules described above. Here, we have made some effort to validate the input, just as an example: we write an error value if we get pas the root node.
use strict;
use warnings;
use feature "say";
# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x
sub parent {
my ($num, $denom) = @{$_[0]};
return ["Error"] if $num == $denom;
return $num < $denom ? [$num, $denom - $num] : [$num - $denom, $denom];
}
for my $fraction ([5, 2], [2, 5], [3, 4], [3, 5], [2, 1], [1, 1]) {
die "Invalid input node @$fraction" if $$fraction[0] == $$fraction[1];
my $parent = parent $fraction;
my $gd_parent = parent $parent;
say "for child @$fraction, parent is @$parent and gd-parent is @$gd_parent";
}
This program displays the following output:
$ perl ./fraction-tree.pl
for child 5 2, parent is 3 2 and gd-parent is 1 2
for child 2 5, parent is 2 3 and gd-parent is 2 1
for child 3 4, parent is 3 1 and gd-parent is 2 1
for child 3 5, parent is 3 2 and gd-parent is 1 2
for child 2 1, parent is 1 1 and gd-parent is Error
Invalid input node 1 1 at fraction-tree.pl line 15.
Curious Fraction Tree in Some Other Programming Languages
In Ring
Again the same rules as before, with an attempt to handle gracefully some of the exceptions:
# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x
for test in [ [5, 2], [2, 5], [3, 4], [3,5], [6, 2], [1, 2] ]
parent = find_parent(test[1], test[2])
gd_parent = find_parent(parent[1], parent[2])
see "Node " + to_str(test) + " has parent " + to_str(parent) +
" and grand-parent " + to_str(gd_parent) + nl
next
func find_parent num, denom
if num < denom
return [num, denom - num]
but denom < num
return [num - denom, denom]
else
return ["Error", ""]
ok
func to_str input
return "" + input[1] + " " + input[2]
This script displays the following output:
$ ring ./fraction-tree.ring
Node 5 2 has parent 3 2 and grand-parent 1 2
Node 2 5 has parent 2 3 and grand-parent 2 1
Node 3 4 has parent 3 1 and grand-parent 2 1
Node 3 5 has parent 3 2 and grand-parent 1 2
Node 6 2 has parent 4 2 and grand-parent 2 2
Node 1 2 has parent 1 1 and grand-parent Error
In Python
No attempt here to validate the input.
# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x
def find_parent(num, denom):
return [num, denom - num] if num < denom else [num - denom, denom]
for test in ([5, 2], [2, 5], [3, 4], [3, 5]):
parent = find_parent(test[0], test[1])
gd_parent = find_parent(parent[0], parent[1])
print("Node", test, "has parent", parent, "and grand-parent", gd_parent)
Output:
$ python3 ./fraction-tree.py
Node [5, 2] has parent [3, 2] and grand-parent [1, 2]
Node [2, 5] has parent [2, 3] and grand-parent [2, 1]
Node [3, 4] has parent [3, 1] and grand-parent [2, 1]
Node [3, 5] has parent [3, 2] and grand-parent [1, 2]
In Julia
Limited attempt to validate the input (catching only some of the exceptions).
function find_parent(num, denom)
return num < denom ? [num, denom - num] :
num > denom ? [num - denom, denom] :
("Error on node $num $denom");
end
for test in [ [5, 2], [2, 5], [3, 4], [3, 5], [1, 2] ]
parent = find_parent(test[1], test[2])
gd_parent = find_parent(parent[1], parent[2])
println("Node $test has parent $parent and grand-parent $gd_parent")
end
Output:
# Node [5, 2] has parent [3, 2] and grand-parent [1, 2]
# Node [2, 5] has parent [2, 3] and grand-parent [2, 1]
# Node [3, 4] has parent [3, 1] and grand-parent [2, 1]
# Node [3, 5] has parent [3, 2] and grand-parent [1, 2]
# Node [1, 2] has parent [1, 1] and grand-parent Error on node
In Awk:
# Run for example as:
# echo ' 5/2
# 2/5
# 3/5' | awk -f fraction-tree.awk
function parent()
{
if (a < b) {
b = b - a
} else {
a = a - b
}
}
BEGIN {
a = 0
b = 0
FS = "/"
}
{
a = $1
b = $2
printf "Node = %d/%d: ", a, b
parent()
printf "Parent = %d/%d; ", a, b
parent()
printf "Grand-parent = %d/%d\n", a, b
}
Output:
$ echo ' 5/2
2/5
3/4
3/5
6/2 ' | awk -f fraction-tree.awk
Node = 5/2: Parent = 3/2; Grand-parent = 1/2
Node = 2/5: Parent = 2/3; Grand-parent = 2/1
Node = 3/4: Parent = 3/1; Grand-parent = 2/1
Node = 3/5: Parent = 3/2; Grand-parent = 1/2
Node = 6/2: Parent = 4/2; Grand-parent = 2/2
In Ruby
# For a node `x/y` with a fraction less than 1, the parent is `x/(y-x)`;
# For a node `x/y` with a fraction larger than 1, the parent is `(x-y)/x`.
def get_parent (pair)
num = pair[0]
denom = pair[1]
return num < denom ? [num, denom - num] : [num - denom, denom];
end
tests = [ [5, 2], [2, 5], [3, 4], [3,5] ]
for test in tests
parent = get_parent(test)
gd_parent = get_parent(parent)
print("Node #{test} - Parent: #{parent} - Grand-Parent: #{gd_parent}\n")
end
Output:
Node 5,2 - Parent: 3,2 - Grand-Parent: 1,2
Node 2,5 - Parent: 2,3 - Grand-Parent: 2,1
Node 3,4 - Parent: 3,1 - Grand-Parent: 2,1
Node 3,5 - Parent: 3,2 - Grand-Parent: 1,2
In Lua
-- For a node `x/y` with a fraction less than 1, the parent is `x/(y-x)`;
-- For a node `x/y` with a fraction larger than 1, the parent is `(x-y)/x`.
local function get_parent(pair)
num = pair[1]
denom = pair[2]
-- no ternary operator in Lua, we can simulate it with and / or:
return num < denom and {num, denom - num} or {num - denom, denom}
end
local function to_str(pair)
-- return pair[1] .. "/" .. pair[2]
return table.concat(pair, "/")
end
local tests = { {5, 2}, {2, 5}, {3, 4}, {3,5} }
for _, test in pairs(tests) do
parent = get_parent(test)
gd_parent = get_parent(parent)
print("Node " .. to_str(test) .. " - Parent: " .. to_str(parent)
.. " - Grand-Parent: " .. to_str(gd_parent))
end
Output:
$ lua ./fraction-tree.lua
Node 5/2 - Parent: 3/2 - Grand-Parent: 1/2
Node 2/5 - Parent: 2/3 - Grand-Parent: 2/1
Node 3/4 - Parent: 3/1 - Grand-Parent: 2/1
Node 3/5 - Parent: 3/2 - Grand-Parent: 1/2
In Kotlin
fun find_parent(pair: IntArray): IntArray {
val num = pair[0]
val denom = pair[1]
return if (num < denom) intArrayOf(num, denom - num) else intArrayOf(num - denom, denom)
}
fun n2str (pair: IntArray): String {
return "${pair[0]}/${pair[1]}"
}
fun main() {
val tests = arrayOf(intArrayOf(5,2), intArrayOf(2,5), intArrayOf(3,4))
for (test in tests) {
val parent = find_parent(test)
val gd_parent = find_parent(parent)
print(n2str(test) + " - Parent: " + n2str(parent))
println(" - Grand-parent: " + n2str(gd_parent))
}
}
Output:
5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1
In C
#include <STDIO>
void parent(int *a, int *b) {
if (*a < *b) {
*b -= *a;
} else {
*a -= *b;
}
}
int main (void) {
int num, denom;
while (scanf ("%d/%d", &num, &denom) == 2) {
printf("%d/%d - ", num, denom);
parent(&num, &denom);
printf("Parent: %d/%d - ", num, denom);
parent(&num, &denom);
printf("Grand-parent: %d/%d \n", num, denom);
}
return (0);
}
Output:
$ echo ' 5/2
2/5
3/4
3/5' | ./a.out
5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1
3/5 - Parent: 3/2 - Grand-parent: 1/2
In Scala
object fraction_tree extends App {
def findParent(pair: List[Int]): List[Int] = {
val num = pair(0)
val denom = pair(1)
return if (num < denom) List(num, denom - num) else List(num - denom, denom)
}
def n2str(pair: List[Int]): String = {
return s"${pair(0)}" + "/" + s"${pair(1)}"
}
val tests: List[List[Int]] = List(List(5, 2), List(2, 5), List(3, 4))
for (test <- tests) {
val parent = findParent(test)
val gd_parent = findParent(parent)
println(n2str(test) + " - Parent: " + n2str(parent) + " - Grand-parent: " + n2str(gd_parent))
}
}
Output:
5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1
Wrapping up
The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on January 16, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.


 I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.
I am the author of the "Think Perl 6" book (O'Reilly, 2017) and I blog about the Perl 5 and Raku programming languages.