These are some answers to the Week 153 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on February 27, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Left Factorials

Write a script to compute Left Factorials of 1 to 10. Please refer OEIS A003422 for more information.

Expected Output:

1, 2, 4, 10, 34, 154, 874, 5914, 46234, 409114

The task specification unfortunately lacks a precise definition of left factorials. Looking at OEIS A003422, I found we could use the following recursive definition:

a(0) = 0
a(1) = 1
a(n) = n*a(n - 1) - (n - 1)*a(n - 2)

After I did some of the implementations below, I found another definition making more sense of left factorials (a.k.a. factorial sums). Left factorial of the integer n is the sum of the factorials of the integers from 0 to n - 1. Left factorial is commonly denoted by a prefixed exclamation mark. So we have:

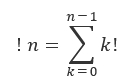
with ! 0 = 0.

Left Factorials in Raku

The implementation can easily be derived from the recursive definition above, except that I prefer an iterative implementation (well, it could probably be argued it is sort of a cached recursive approach, even though there is no recursive subroutine call):

my @a = 0, 1, 2;
for 3..10 -> $n {
    @a[$n] = $n * @a[$n -1] - ($n - 1) * @a[$n - 2];
}
say @a[1..10];

This program displays the following output:

$ raku ./left_fact.raku
(1 2 4 10 34 154 874 5914 46234 409114)

In Raku, we can also use sigilless variables) to make the code look more like a math formula:

my @a = 0, 1;
for 2..10 -> \n {
    @a[n] = n * @a[n -1] - (n - 1) * @a[n - 2];
}
say @a[1..10];

This new version displays the same output.

As mentioned before, the above implementations were done before I found about the second (summation of factorials) formula. Raku has reduction metaoperators) making it easy to implement factorials and summations. This can lead to this concise Raku one-liner using two triangular reduction operators:

$ raku -e 'say (|[\+] 1, (|[\*] 1..*))[0..9]'
(1 2 4 10 34 154 874 5914 46234 409114)

In addition, we could also define a prefix ! operator, but this has the drawback of redefining the standard negation prefix operator !. This does work, but it’s probably not very wise to do so.

Left Factorials in Perl

Again, the implementation can easily be derived from the recursive definition provided above:

use strict;
use warnings;
use feature "say";

my @a = (0, 1);
for my $n (2..10) {
    $a[$n] = $n * $a[$n -1] - ($n - 1) * $a[$n - 2];
}
say "@a[1..10]";

This program displays the following output:

$ perl ./left_fact.pl
1 2 4 10 34 154 874 5914 46234 409114

Left Factorials in Other Languages

In Julia

Using the recursive definition of left factorials:

a = [1, 2] # Julia arrays start with index 1

for n in 3:10
    push!(a, n * a[n - 1] - (n - 1) * a[n - 2])
end
println(a)

Output:

$ julia ./left_fact.jl
[1, 2, 4, 10, 34, 154, 874, 5914, 46234, 409114]

In Ring

Here, we use the summation of factorials definition. For each iteration in the for loop, we multiply fact by the loop variable to obtain the new factorial, and we add the new factorial to the sum variable. For some strange reason, see left_fact + " "' doesn’t output a space after the variable value, where as see " " + left_fact does what we want. To me, it looks like a small bug in the language, but I may be missing something.

left_fact = 1
fact = 1
for i = 1 to 10
    see " " + left_fact 
    fact *= i
    left_fact += fact  
next
see " " + nl

Output:

$ ring ./left_fact.ring
1 2 4 10 34 154 874 5914 46234 409114

In Python

Again using the summation of factorials definition.

fact = 1
left_fact = 1

for n in range (1, 11):
    print(left_fact)
    fact = fact * n
    left_fact = left_fact + fact

Output:

$ python3 ./left_fact.py
1
2
4
10
34
154
874
5914
46234
409114

Note that I didn’t remember how to how to output data without a new line in Python, and I was too lazy to spend time to find out. This is proverbially left as an exercise to the reader, as this output fits the specification bill.

In Awk

Using the summation of factorials definition.

BEGIN {
    left_fact = 1
    fact = 1
    for (i = 1; i <= 10; i++) {
        printf "%d ", left_fact
        fact *= i
        left_fact += fact  
    }
    printf "\n"
}

Output:

$ awk -f left_fact.awk
1 2 4 10 34 154 874 5914 46234 409114

In C

Using the summation of factorials definition.

#include <stdio.h>

int main () {
    int sum = 1;
    int fact = 1;
    for (int i = 1; i <= 10; i++) {
        printf("%d ", sum);
        fact *= i;
        sum += fact;
    }
    printf ("\n");
    return 0;
}

Output:

$ ./test-left
1 2 4 10 34 154 874 5914 46234 409114

In Bc

Using the summation of factorials definition.

sum = 1
fact = 1

for (n = 1; n <= 10; n ++) {
    print sum, " "
    fact = fact * n
    sum = sum + fact
}

Output:

$ bc left_fact.bc
bc 1.06.95
Copyright (...)
1 2 4 10 34 154 874 5914 46234 409114

In Tcl

Using the summation of factorials definition.

set left_fact 1
set fact 1
puts -nonewline $left_fact

for {set i 1} {$i <= 10} {incr i} {
    puts -nonewline "${left_fact} "
    set fact [expr $fact * $i]
    set left_fact [expr $left_fact + $fact]

}
puts ""

Output:

$ tclsh ./left_fact.tcl
11 2 4 10 34 154 874 5914 46234 409114

In R

Using the summation of factorials definition.

left_fact <- 1
fact <- 1

for (i in 1:10) {
    cat(left_fact, '')
    fact <- fact * i
    left_fact <- left_fact + fact
}
cat("\n")

Output:

$ Rscript left_fact.r
1 2 4 10 34 154 874 5914 46234 409114

In Pascal

Using the summation of factorials definition.

Program leftfact;

var
    fact, left_fact: longint;
    i: integer;

begin
    left_fact := 1;
    fact := 1;
    for i := 1 to 10 do begin
        write(left_fact, ' ');
        fact := fact * i;
        left_fact := left_fact + fact;
    end;
    writeln('');
end.

Output:

$ ./left_fact
1 2 4 10 34 154 874 5914 46234 409114

In Rust

Using the summation of factorials definition.

fn main() {
    let mut fact = 1;
    let mut left_fact = 1;
    for n in 1..11 {
        println!("{}", left_fact);
        fact = fact * n;
        left_fact = left_fact + fact;
    }
}

Output:

$ ./left_fact
1
2
4
10
34
154
874
5914
46234
409114

In Go

Using the summation of factorials definition.

package main

import "fmt"

func main() {
    left_fact := 1
    fact := 1
    for i := 1; i <= 10; i++ {
        fmt.Printf("%d ", left_fact)
        fact *= i
        left_fact += fact
    }
    fmt.Printf("\n")
}

Output:

1 2 4 10 34 154 874 5914 46234 409114

In Scala

Using the summation of factorials definition.

object fact_left extends App {
  var fact = 1
  var left_fact = 1
  for (n <- 1 to 10) {
    println(left_fact)
      fact *= n
    left_fact += fact
  }
}

Output: 1 2 4 10 34 154 874 5914 46234 409114

In Ruby

Using the summation of factorials definition.

fact = 1
left_fact = 1
for n in 1..10 
    printf "%d ", left_fact
    fact *= n
    left_fact += fact
end
printf "\n"

Output:

ruby left_fact.rb
1 2 4 10 34 154 874 5914 46234 409114

In Lua

Using the summation of factorials definition.

fact = 1
left_fact = 1
for n = 1, 10 do
    print(left_fact)
    fact = fact * n
    left_fact = left_fact + fact
end

Output:

$ lua left_fact.lua
1
2
4
10
34
154
874
5914
46234
409114

In Kotlin

Using the summation of factorials definition.

fun main() {
    var fact = 1
    var left_fact = 1
    for (i in 1..9) {
        fact *= i
        left_fact += fact
        print("$left_fact ")
    }
}

Output:

$ ./left_fact.kexe
2 4 10 34 154 874 5914 46234 409114

Task 2: Factorions

You are given an integer, $n.

Write a script to figure out if the given integer is factorion.

A factorion is a natural number that equals the sum of the factorials of its digits.

Example 1:

Input: $n = 145
Output: 1

    Since 1! + 4! + 5! => 1 + 24 + 120 = 145

Example 2:

Input: $n = 123
Output: 0

    Since 1! + 2! + 3! => 1 + 2 + 6 <> 123

We will slightly deviate from the task specification and write a subroutine that checks whether an integer is a factorion, and write a program to find all factorions in a given range.

Factorions in Raku

Here again, we use twice the reduction metaoperators), one ([*] 1..$_) to compute the factorial of a digit, and one ([+]) to sum up the digit factorials.

sub is_factorion (Int $in) {
    my $sum = [+] map { [*] 1..$_ }, $in.comb;
    return $sum == $in;
}
say $_ if is_factorion $_ for 1..50000;

We chose here an upper limit of 50,000 because it is known and proven that there are only 4 factorions in the decimal system, all smaller than 50,000. This solution is concise and elegant and the is_factorion subroutine could easily be boiled down to a single code line:

sub is_factorion (Int $in) {
    return $in == [+] map { [*] 1..$_ }, $in.comb;
}

This program displays the following output:

$ time raku ./factorion.raku
1
2
145
40585

real    0m13,079s
user    0m0,015s
sys     0m0,030s

Note that I timed the execution because I felt it was a bit slow. The reason for that slowness is that we’re computing the factorial of each digit a very large number of times. It is significantly more efficient to cache the factorials of each digit, for example by storing in an array (@fact) the precomputed factorials of digits 0 to 9.

my @fact = map { [*] 1..$_ }, 0..9;
sub is_factorion (Int $in) {
    my $sum = [+] map { @fact[$_] }, $in.comb;
    return $sum == $in;
}
say $_ if is_factorion $_ for 1..50000;

This modified program displays the following output and timings:

$ time raku ./factorion.raku
1
2
145
40585

real    0m1,553s
user    0m0,000s
sys     0m0,015s

So caching the digit factorials made the program about 8.5 times faster.

Factorions in Perl

In Perl, we implemented directly the cached version with a @digit_fact array:

use strict;
use warnings;
use feature "say";

sub fact {
    my $i = shift;
    my $prod = 1;
    $prod *= $_ for 2..$i;
    return $prod;
}

my @digit_fact = map {fact $_} 0..9;

sub is_factorion {
    my $in = shift;
    my $sum = 0;
    $sum += $_ for map { $digit_fact[$_] } split //, $in;
    return $sum == $in;
    #say $sum;
}
for (1..50000) {
    say $_ if is_factorion($_)
}

This program displays the following output:

$ time perl ./factorion.pl
1
2
145
40585

real    0m0,182s
user    0m0,140s
sys     0m0,015s

Factorions in Other Languages

In Julia

fact = map(x -> factorial(x), Vector(0:9))

function is_factorion(num)
    sum = 0
    start_num = num
    for n in 1:length(string(num))
        sum += fact[num % 10 + 1] # Julia arrays start at 1
        num = num ÷ 10
    end
    return sum == start_num
end

for i in 1:50000
    if is_factorion(i)
        println(i)
    end
end

Output:

$ julia ./factorion.jl
1
2
145
40585

In Ring

In Ring, list index starts at 1. That makes index management a bit complicated in this case, because we need to store the factorial of 0. So factorial 0 is stored at index 1, and all the others are shifted by 1. It’s not a problem, but it makes the code look a bit unnatural.

fact = [1, 1]
for k = 2 to 9
    add (fact, k * fact[k]) # list indices start at 1
next
# see fact + nl
for n = 1 to 50000
    if is_factorion(fact, n)
        see n + nl
    ok
next

func is_factorion fact, input
    sum = 0
    n = "" + input
    for i = 1 to len(n)
        digit = n[i]
        sum += fact[1 + digit]
    next
    return input = sum

Output:

$ ring ./factorion.ring
1
2
145
40585

In Python

fact = [1] * 10
for n in range (1, 10):
    fact[n] = n * fact[n - 1]

def is_factorion (input):
    sum = 0
    n = str(input)
    for i in range (0, len(n)):
        sum = sum + fact[int(n[i])]

    return input == sum

for n in range(1, 50000):
    if is_factorion(n):
        print(n)

Output:

$ python3 ./factorion.py
1
2
145
40585

In C

#include <stdio.h>

char is_factorion(int fact[], int num) {
    int sum = 0;
    int n = num;
    while (n > 0) {
        sum += fact[n % 10];
        n /= 10;
    }
    return num == sum;
}

int main() {
    int fact[10];
    fact[0] = 1;
    for (int i = 1; i <= 9; i++) {
        fact[i] = i * fact[i - 1];
    }

    for (int n = 1; n < 50000; n++) {
        if (is_factorion(fact, n)) {
            printf("%d ", n);
        }
    }
    printf("\n");
    return 0;
}

Output:

$ ./factorion 1 2 145 40585

In Awk

function populate_fact() {
    fact[0] = 1
    for (n = 1; n <= 9; n++) {
        fact[n] = n * fact[n - 1]
    }
}
function is_factorion(num) {
    sum = 0
    start_num = num
    for (n = 0; n < length(start_num); n++) {
        sum += fact[num % 10]
        num = int(num / 10)
    }
    return sum == start_num
 }
BEGIN {
    populate_fact()
    for (i = 1; i <= 50000; i++) {
        if (is_factorion(i)) {
            print i
        }
    }
}

Output:

$ awk -f factorion.awk
1
2
145
40585

In Bc

fact[0] = 1
for (n = 1; n <= 9; n++) {
    fact[n] = n * fact[n - 1]
}
for (n = 1; n <= 50000; n++) {
    sum = 0
    i = n
    while (i > 0) {
        sum += fact[i % 10]
        i /= 10
    }
    if (sum == n) {
        print n, " "
    }
}
halt

Output:

$ bc  factorion.bc
bc 1.06.95
Copyright (...)
1 2 145 40585

In Scala

object factorion extends App {
  def is_factorion(fact: Array[Int], num: Int): Boolean = {
    var sum = 0
    var i = num
    while (i > 0) {
      sum += fact(i % 10)
      i /= 10
    }
    return num == sum
  }

  val fact = new Array[Int](12)
  fact(0) = 1
  for (n <- 1 to 9) {
    fact(n) = n * fact(n - 1)
  }

  for (j <- 1 to 50000) {
    if (is_factorion(fact, j)) {
      println(j)
    }
  }
}

Output:

1
2
145
40585

In Lua

function is_factorion(fact, num)
    sum = 0
    i = num
    while i > 0 do
        sum = sum + fact[ 1 + i % 10]
        i = math.floor(i / 10)
    end
    return num == sum
end

fact = {1}
for n = 1, 10 do
    table.insert(fact, n * fact[n])
end
for j = 1, 50000 do
    if is_factorion(fact, j) then
        print(j)
    end
end

Output:

$ lua factorion.lua
1
2
145
40585

In Kotlin

fun main() {
    var fact = mutableListOf<Int>()
    fact.add(1)
    for (n in 1..9) {
        fact.add(n * fact[n-1])
    }
    for (num in 1..50000) {
        var i = num
        var sum = 0
        while (i > 0) {
            sum += fact[i % 10]
            i /= 10
        }
        if (num == sum) print ("$num ")
    }
}

Output:

$ ./factorion.kexe
1 2 145 40585

In Ruby

def is_factorion(fact, num)
    sum = 0
    i = num
    while i > 0
        i, d = i.divmod(10)
        sum += fact[d]
    end
    return num == sum
end

fact = [1]
for n in 1..10
    fact.push(n * fact[n - 1])
end
for j in 1..50000
    if is_factorion(fact, j)
        printf "%d ", j
    end
end
printf("\n")

Output:

$ ruby factorion.rb
1 2 145 40585

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on March 6, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.

These are some answers to the Week 151 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Task 1: Binary Tree Depth

You are given binary tree.

Write a script to find the minimum depth.

The minimum depth is the number of nodes from the root to the nearest leaf node (node without any children).

Example 1:

Input: '1 | 2 3 | 4 5'

                1
               / \
              2   3
             / \
            4   5

Output: 2

Example 2:

Input: '1 | 2 3 | 4 *  * 5 | * 6'

                1
               / \
              2   3
             /     \
            4       5
             \
              6
Output: 3

The first obvious way to solve this task is to build the tree from the input string and then to walk through it to find the minimum depth. I’ve decided to try another approach: scan the input string to try to find directly the minimum depth. I think this approach works fine, but I may have missed some edge case. I wish I could explain the idea with more details, but I’m running out of time.

Binary Tree Depth in Raku

use v6;

sub min-depth (Str $tree) {
    my @ranks = split /'|'/, $tree;
    return "depth: 1" if @ranks == 1;
    for 1..@ranks.end -> $i {
        my @nodes = @ranks[$i] ~~ m:g/'*' | \d+/;
        return "depth: {$i}" if @nodes.elems + 1 < 2 ** $i and $i == @ranks.end;
        return "depth: {$i+1}" if @nodes.elems + 1 <= 2 ** $i ;
        for (@ranks[$i]).comb(/\S+/) -> $a, $b {
            return "depth: $i" if $a eq $b eq '*';
        }
    return "depth: {$i+1}" if $i == @ranks.end;
    }
}

for '1 ',   '1 |',   '1 | 2 3', 
    '1 | 2 3 | 4 5', 
    '1 | 2 3 | 4 *  * 5 | * 6',
    '1 | 2 3 | * *  4 5 | * * 6',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 14 ',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 ',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 '
    -> $test {
    printf "%-45s -> %s\n", "'$test'", min-depth $test
}

This program displays the following output:

$ raku ./min_depth.raku
'1 '                                          -> depth: 1
'1 |'                                         -> depth: 1
'1 | 2 3'                                     -> depth: 2
'1 | 2 3 | 4 5'                               -> depth: 2
'1 | 2 3 | 4 *  * 5 | * 6'                    -> depth: 3
'1 | 2 3 | * *  4 5 | * * 6'                  -> depth: 2
'1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 14 '   -> depth: 4
'1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 '      -> depth: 4
'1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 '         -> depth: 3

Binary Tree Depth in Perl

use strict;
use warnings;
use feature "say";

sub min_depth {
    my $tree = shift;
    my @ranks = split /\|/, $tree;
    return "depth: 1" if @ranks == 1;
    for my $i (1..$#ranks) {
        # say $ranks[$i];
        my @nodes = ($ranks[$i] =~ /\*|\d+/g);
        # say "@nodes";
        return "depth: $i" if @nodes + 1 < 2 ** $i and $i == $#ranks;
        return "depth: " . ($i+1) if @nodes + 1 <= 2 ** $i ;
        my $j = 0;
        while ($j <= $#nodes) {
            return "depth: $i" if $nodes[$j] eq '*' and $nodes[$j+1] eq '*';
            $j += 2;
        }
        return "depth: ". ($i + 1) if $i + 1 == @ranks;
    }
}

for my $test ( '1 ',   '1 |',   '1 | 2 3', 
    '1 | 2 3 | 4 5', 
    '1 | 2 3 | 4 *  * 5 | * 6',
    '1 | 2 3 | * *  4 5 | * * 6',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 14 ',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 ',
    '1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 ' ) {
        printf "%-42s -> %s\n", "$test", min_depth($test);
}

This program displays the following output:

$ perl  ./min-depth.pl
1                                          -> depth: 1
1 |                                        -> depth: 1
1 | 2 3                                    -> depth: 2
1 | 2 3 | 4 5                              -> depth: 2
1 | 2 3 | 4 *  * 5 | * 6                   -> depth: 3
1 | 2 3 | * *  4 5 | * * 6                 -> depth: 2
1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13 14   -> depth: 4
1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12 13      -> depth: 4
1 | 2 3 | 4 4 5 6 | 7 8 9 10 11 12         -> depth: 3

Task 2: Rob the House

You are planning to rob a row of houses, always starting with the first and moving in the same direction. However, you can’t rob two adjacent houses.

Write a script to find the highest possible gain that can be achieved.

Example 1:

Input: @valuables = (2, 4, 5);
Output: 7

If we rob house (index=0) we get 2 and then the only house we can rob is house (index=2) where we have 5.
So the total valuables in this case is (2 + 5) = 7.

Example 2:

Input: @valuables = (4, 2, 3, 6, 5, 3);
Output: 13

The best choice would be to first rob house (index=0) then rob house (index=3) then finally house (index=5).
This would give us 4 + 6 + 3 =13.

Rob the House in Raku

We use a get_best recursive subroutine to explore all combinations of values, except that we don’t need to look ahead more than 2 values.

use v6;

sub get_best(@in, $sum-so-far is copy) {
    if @in.elems <= 2  {
        $sum-so-far += @in.max;
        $*best-so-far = $sum-so-far if $sum-so-far > $*best-so-far;
        return;
    }      
    for 0, 1 -> $i {
        get_best @in[$i + 2 .. @in.end], $sum-so-far + @in[$i];
    }
}
my @valuables = (2, 4, 5), (4, 2, 3, 6, 5, 3), (4, 2, 5, 10);
for @valuables -> $test {
    my $*best-so-far = 0;  # dynamic scope variable
    get_best $test, 0;
    say $test, " -> ", $*best-so-far;
}

This program displays the following output:

$ raku ./robber.raku
(2 4 5) -> 7
(4 2 3 6 5 3) -> 13
(4 2 5 10) -> 14

Rob the House in Perl

We also use a get_best recursive subroutine to explore all combinations of values.

use strict;
use warnings;
use feature "say";

my $best_so_far;

sub get_best {
    my $sum_so_far = $_[0];
    my @in = @{$_[1]};

    if (@in <= 2)  {
        $sum_so_far += $in[0] if @in == 1;
        $sum_so_far += $in[1] if @in == 2;    
        $best_so_far = $sum_so_far if $sum_so_far > $best_so_far;
        return;
    }
    for my $i (0, 1) {
        get_best($sum_so_far + $in[$i], [@in[$i + 2 .. $#in]]);
    }
}

my @valuables = ([2, 4, 5], [4, 2, 3, 6, 5, 3], [4, 2, 5, 10]);
for my $test (@valuables) {
    $best_so_far = 0; 
    get_best 0, $test;
    say "@$test -> ", $best_so_far;
}

This program displays the following output:

$ perl ./robber.pl
2 4 5 -> 7
4 2 3 6 5 3 -> 13
4 2 5 10 -> 14

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on February 20, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.

These are some answers to the Week 149 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on February 6, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: Fibonacci Words

You are given two strings having same number of digits, $a and $b.

Write a script to generate Fibonacci Words by concatenation of the previous two strings. Finally print 51st digit of the first term having at least 51 digits.

Example:

Input: $a = '1234' $b = '5678'
Output: 7

Fibonacci Words:

'1234'
'5678'
'12345678'
'567812345678'
'12345678567812345678'
'56781234567812345678567812345678'
'1234567856781234567856781234567812345678567812345678'

The 51st digit in the first term having at least 51 digits '1234567856781234567856781234567812345678567812345678' is 7.

So, Fibonacci words are similar to Fibonacci numbers, except that any value is generated by concatenating (instead of adding) the two previous values.

Since we can easily find how many digits we add each time through the iteration, there is certainly a way to find directly the requested digit without even computing the sequence’s words, but it is much simpler to iteratively compute the words and pick up the 51st digit once we have enough digits for that.

Fibonacci Words in Raku

Here, we use the sequence operator to generate a sequence of Fibonacci words. We stop the sequence with the *.chars >= 51 expression. We then just take the digit at index 50 (corresponding to position 51) of the last word.

use v6;

sub fibonacci (Int $a, Int $b where $a.chars == $b.chars) {
    my ($c, $d) = $a < $b ?? ($a, $b) !! ($b, $a);
    my @fib = $c, $d, * ~ * ... *.chars >= 51;
    # say @fib;
}
say (fibonacci 1234, 5678)[*-1].comb[50];

This script displays the following output:

$ raku ./Fibonacci_words.raku
7

Fibonacci Words in Perl

Same idea as above, except that we build the sequence of Fibonacci words with a for loop.

use strict;
use warnings;
use feature "say";

sub fibonacci {
    my ($a, $b) = @_;
    my @fib = $a < $b ? ($a, $b) : ($b, $a);
    for my $i (1..20) {
        push @fib, $fib[-2] . $fib[-1];
        next if length $fib[-1] < 51;
        say $fib[-1];
        return $fib[-1];
    }
}
say substr fibonacci(1234, 5678), 50, 1;

This script displays the following output:

$ perl ./Fibonacci_words.pl
1234567856781234567856781234567812345678567812345678
7

Task 2: Square-Free Integers

Write a script to generate all square-free integers <= 500.

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no perfect square other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 x 5 is square-free, but 18 = 2 x 3 x 3 is not, because 18 is divisible by 9 = 32.

Example:

The smallest positive square-free integers are:

1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, ...

The first idea that might come to mind would be to perform prime factorization of all integers between 2 and 500, and to retain all those whose all exponents are 1. But that’s a lot of computing work, much of which is in fact useless. It is much better to try to divide the input integers by perfect squares. Why would you want to test twice division by 2 when it is enough to test once division by 4? Only six squares of prime numbers may occur in prime factorization of integers below 500: 4, 9, 25, 49, 121, 169. There are some other squares (such as 16, 36, 64, 81, 100, 144, 196, and 225), but these are not squares of prime numbers and numbers containing these squares will all have been found to contain squares when we test 4, 9, and 25.

Square-Free Integers in Raku

We first need to build a list of squares of prime numbers less than the square root of 500/2. For each integer between 1 and 500, we test whether any of the squares evenly divides that integer. A small easy optimization is that we can stop the process whenever we reach a square larger than the integer being tested.

my @squares = map { $_² }, grep {.is-prime}, 2..250.sqrt.Int;
# say @squares; # [4 9 25 49 121 169] squares of prime integers
NEXT_I: for 1..500 -> $i {
    for @squares -> $j {
        next NEXT_I if $i %% $j;
        last if $j > $i;
    }
    print "$i ";
}
say "\nDuration: ", now - INIT now;

This script displays the following output:

$ raku ./square-free.raku
1 2 3 5 6 7 10 11 13 14 15 17 19 21 22 23 26 29 30 31 33 34 35 37 38 39 41 42 43 46 47 51 53 55 57 58 59 61 62 65 66 67 69 70 71 73 74 77 78 79 82 83 85 86 87 89 91 93 94 95 97 101 102 103 105 106 107 109 110 111 113 114 115 118 119 122 123 127 129 130 131 133 134 137 138 139 141 142 143 145 146 149 151 154 155 157 158 159 161 163 165 166 167 170 173 174 177 178 179 181 182 183 185 186 187 190 191 193 194 195 197 199 201 202 203 205 206 209 210 211 213 214 215 217 218 219 221 222 223 226 227 229 230 231 233 235 237 238 239 241 246 247 249 251 253 254 255 257 258 259 262 263 265 266 267 269 271 273 274 277 278 281 282 283 285 286 287 289 290 291 293 295 298 299 301 302 303 305 307 309 310 311 313 314 317 318 319 321 322 323 326 327 329 330 331 334 335 337 339 341 345 346 347 349 353 354 355 357 358 359 361 362 365 366 367 370 371 373 374 377 379 381 382 383 385 386 389 390 391 393 394 395 397 398 399 401 402 403 406 407 409 410 411 413 415 417 418 419 421 422 426 427 429 430 431 433 434 435 437 438 439 442 443 445 446 447 449 451 453 454 455 457 458 461 462 463 465 466 467 469 470 471 473 474 478 479 481 482 483 485 487 489 491 493 494 497 498 499

Duration: 0.12648938

We compute and display the duration just to check that the program runs fast enough.

Square-Free Integers in Perl

This is the same idea as explained above. A slight change is that this program doesn’t test for primality of the numbers that will be squared, because anyone with only basic math knowledge can list prime numbers between 1 and 15. So we don’t need to compute them, we simply hard-code them.

use strict;
use warnings;
use feature "say";

my @squares = map { $_ * $_ } 2, 3, 5, 7, 11, 13;
# say "@squares"; # 4 9 25 49 121 169 - squares of prime integers
NEXT_I: for my $i (1..500) {
    for my $j (@squares) {
        next NEXT_I if $i % $j == 0;
        last if $j > $i;
    }
    print "$i ";
}
say " ";

This script displays the following output:

$ perl ./square-free.pl
1 2 3 5 6 7 10 11 13 14 15 17 19 21 22 23 26 29 30 31 33 34 35 37 38 39 41 42 43 46 47 51 53 55 57 58 59 61 62 65 66 67 69 70 71 73 74 77 78 79 82 83 85 86 87 89 91 93 94 95 97 101 102 103 105 106 107 109 110 111 113 114 115 118 119 122 123 127 129 130 131 133 134 137 138 139 141 142 143 145 146 149 151 154 155 157 158 159 161 163 165 166 167 170 173 174 177 178 179 181 182 183 185 186 187 190 191 193 194 195 197 199 201 202 203 205 206 209 210 211 213 214 215 217 218 219 221 222 223 226 227 229 230 231 233 235 237 238 239 241 246 247 249 251 253 254 255 257 258 259 262 263 265 266 267 269 271 273 274 277 278 281 282 283 285 286 287 289 290 291 293 295 298 299 301 302 303 305 307 309 310 311 313 314 317 318 319 321 322 323 326 327 329 330 331 334 335 337 339 341 345 346 347 349 353 354 355 357 358 359 361 362 365 366 367 370 371 373 374 377 379 381 382 383 385 386 389 390 391 393 394 395 397 398 399 401 402 403 406 407 409 410 411 413 415 417 418 419 421 422 426 427 429 430 431 433 434 435 437 438 439 442 443 445 446 447 449 451 453 454 455 457 458 461 462 463 465 466 467 469 470 471 473 474 478 479 481 482 483 485 487 489 491 493 494 497 498 499

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on February 13, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.