laurent_r

These are some answers to the Week 281, Task 2, of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on August 11, 2024, at 23:59). This blog post provides some solutions to this challenge. Please don’t read on if you intend to complete the challenge on your own.

Task 2: Knight’s Move

A Knight in chess can move from its current position to any square two rows or columns plus one column or row away. So in the diagram below, if it starts a S, it can move to any of the squares marked E.

Write a script which takes a starting position and an ending position and calculates the least number of moves required.

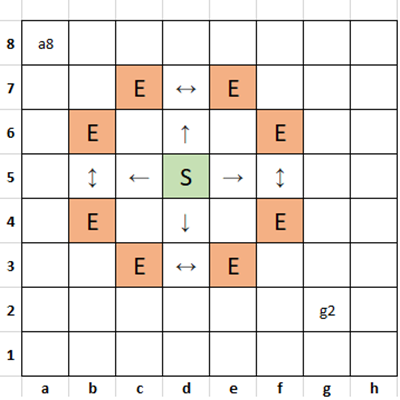
Example 1

Input: $start = 'g2', $end = 'a8'
Ouput: 4

g2 -> e3 -> d5 -> c7 -> a8

Example 2

Input: $start = 'g2', $end = 'h2'
Ouput: 3

g2 -> e3 -> f1 -> h2

This is a classical computer science topic. In fact, I had to implement almost the same task in C and in Pascal as a homework exercise in the beginning of my CS studies many years ago. It is an opportunity to study and understand First-In First-Out (FIFO) data structures such as queues, as opposed to Last-in First Out (LIFO) data structures, aka stacks. It is also an occasion to work on Breadth-First Search (BFS) algorithms (as opposed to Depth-First Search (DFS) algorithms) for creating and traversing a tree.

BFS traverses a tree by visiting all possible moves level by level, so that as soon as we find a solution, we know it is the shortest path (or, rather, one of the shortest paths) and can stop iteration and return the level value. In DFS, by contrast, you would need to explore essentially all possible paths to make sure you've found the shortest one.

A final point before we go on: how do we model the chess board? I considered various solutions and decided to transform the chess notation a to h abscissas to a 0 to 7 range. For the ordinates, we subtract 1 to convert the 1 to 8 range to a 0 to 7 range. For example, the c2 square would be transformed to rectangular or Cartesian coordinates (2, 1). This conversion is performed by the to-coordinates subroutine.

Knight’s Move in Raku

The authorized moves for a knight are modeled by @moves, an array of eight pairs representing the values to be added to the coordinates of one square to find the next square.

The @to-be-explored array contains subarrays describing the next squares to be visited along with the level depth (i.e. the number of moves to reach this square). The @to-be-explored array is initialized with the starting position (and a depth of 0). The %seen hash contains the squares that have already been visited (we simply stringify the pair of coordinates to build the hash key). The %seen hash is also initialized with the starting position.

The process traverses the @to-be-explored array and return the depth if it is the target square. Otherwise, for each item, it computes the next position that would be reached with each of the eight possible moves. This next position is dismissed if it falls out of the chess board (unauthorized move) or if it has already been visited. Else, the next position is added to the %seen hash and to the @to-be-explored array.

my @moves = <2 1>, <2 -1>, <1 2>, <1 -2>, 
            <-1 2>, <-1 -2>, <-2 1>, <-2 -1>;

sub to-coordinates ($in) {
    my ($col, $row) = $in.comb;
    return $col.ord - 'a'.ord, $row - 1;
}

sub find-shortest ($st-in, $end-in) {
    # convert input to Cartesian coordinates
    my @start = to-coordinates $st-in;
    my @end = to-coordinates $end-in;

    my @to-be-explored;  # a queue of squares to be visited    
    push @to-be-explored, (0, @start).flat; 
    my %seen = "@start[]" => 1;  # already visited squares

    while @to-be-explored {
        my @node = shift @to-be-explored;
        my ($depth, @current) = @node[0];
        return $depth if "@current[]" eq "@end[]";
        for @moves -> @move {
            my @next = @current[0] + @move[0], 
                       @current[1] + @move[1];
            # dismiss if computed position not on chessboard
            next if @next.any > 7 or @next.any < 0;
            # dismiss if computed position already visited
            next if %seen{"@next[]"}:exists;
            # update seen hash and to-be-explored queue
            %seen{"@next[]"} = 1;
            push @to-be-explored, ($depth + 1, @next).flat;
        }
    }
}

my @tests = <g2 a8>, <g2 h2>;
for @tests -> @test {
    printf "%-6s => ", "@test[]"; 
    say find-shortest @test[0], @test[1];
}

This program displays the following output:

$ raku ./shortest-knight-path.raku
g2 a8  => 4
g2 h2  => 3

Knight’s Move in Perl

This is a port to Perl of the Raku program above. Please refer to the rather large chunks of information provided in the two sections above if you need further information.

use strict;
use warnings;
use feature 'say';

my @moves = ( [<2 1>], [<2 -1>], [<1 2>], [<1 -2>], 
              [<-1 2>], [<-1 -2>], [<-2 1>], [<-2 -1>] );

sub to_coordinates {
    my ($col, $row) = split //, shift;
    return ord($col) - ord('a'), $row - 1;
}

sub find_shortest  {
    my ($st_in, $end_in) = @_;
    # convert input to Cartesian coordinates
    my @start = to_coordinates $st_in;
    my @end = to_coordinates $end_in;

    my @to_be_explored;  # a queue of squares to be visited    
    push @to_be_explored, [0, @start]; 
    my %seen = ("@start" => 1);  # already visited squares
    while (@to_be_explored) {
        my $node = shift @to_be_explored;
        my ($depth, @current) = @$node;
        return $depth if "@current" eq "@end";
        for my $move (@moves) {
            my @next = ( $current[0] + $move->[0], 
                         $current[1] + $move->[1] );
            # dismiss if computed position not on chessboard
            next if $next[0] > 7 or $next[0] < 0 or
                    $next[1] > 7 or $next[1] < 0;
            # dismiss if computed position already visited
            next if exists $seen{"@next"};
            # update seen hash and to_be_explored queue
            $seen{"@next"} = 1;
            push @to_be_explored, [$depth + 1, @next];
        }
    }
}

my @tests = ([<g2 a8>], [<g2 h2>]);
for my $test (@tests) {
    printf "%-6s => ", "@$test"; 
    say find_shortest @$test;;
}

This program displays the following output:

$ perl  ./shortest-knight-path.pl
g2 a8  => 4
g2 h2  => 3

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on August 18, 2024. And, please, also spread the word about the Perl Weekly Challenge if you can.