E. Choroba

The longest sequence

Generate a longest sequence of the following “English Pokemon” names where each name starts with the last letter of previous name.

I’m not sure whether the term “sequence” has a unique and generally accepted definition. For example, does it have to contain each element just once? If not, the longest sequence might be

girafarig girafarig girafarig girafarig girafarig girafarig girafarig girafarig...

If we want each element to appear just once in the sequence, we are in the graph theory and we search for the longest simple path. For a general graph, this is an NP-hard problem, but fortunately, our input is small enough to be solved in reasonable time.

We can implement a brute-force search (i.e. trying all the possible sequences) recursively. The recursive steps takes the sequence constructed so far and tries to extend it by all the possible next steps, calling itself to extend each of them further.

To speed the program up, the possible neighbours are recorded in a hash %next.

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

my @names = qw( audino bagon baltoy banette bidoof braviary bronzor
                carracosta charmeleon cresselia croagunk darmanitan
                deino emboar emolga exeggcute gabite girafarig gulpin
                haxorus heatmor heatran ivysaur jellicent jumpluff
                kangaskhan kricketune landorus ledyba loudred lumineon
                lunatone machamp magnezone mamoswine nosepass petilil
                pidgeotto pikachu pinsir poliwrath poochyena porygon2
                porygonz registeel relicanth remoraid rufflet sableye
                scolipede scrafty seaking sealeo silcoon simisear
                snivy snorlax spoink starly tirtouga trapinch treecko
                tyrogue vigoroth vulpix wailord wartortle whismur
                wingull yamask );

my %next;
for my $name (@names) {
    @{ $next{$name} }{
        grep substr($name, -1) eq substr($_, 0, 1), @names
    } = ();
}


sub longest_path {
    my @longest_paths = ([]);
    _longest_path([$_], {}, \@longest_paths) for @names;
    shift @longest_paths
        until @{ $longest_paths[0] } == @{ $longest_paths[-1] };  # (1)
    return @longest_paths
}


sub _longest_path {
    my ($so_far, $used, $longest_paths) = @_;
    my @following = grep ! exists $used->{$_},
                    keys %{ $next{ $so_far->[-1] } };
    for my $f (@following) {
        undef $used->{$f};
        push @$so_far, $f;
        _longest_path($so_far, $used, $longest_paths);
        pop @$so_far;
        delete $used->{$f};
    }
    push @$longest_paths, [@$so_far] if @$so_far >= @{ $longest_paths->[-1] };
}


my @longest_paths = longest_path();

say "@$_" for @longest_paths;
say "There are ", scalar @longest_paths,
    " paths of length ", scalar @{ $longest_paths[0] };

The shift at (1) just removes the shorter (shortest-so-far) sequences from the results.

To avoid copying the data, we only pass references around. Therefore, after returning from the recursion, we need to return the structures into their previous state. That’s why there’s pop and delete after the recursive call.

The program finds all the possible 1248 paths of length 23 in less than 10 seconds.

Unique edges

What if we changed the definition of the term “sequence” so that the elements might be repeated, but each pair (or edge in the graph theory parlance) must be used just once?

We can reuse our program if we first construct a line graph from our graph: its vertices correspond to edges in the original graph. Unfortunately, such a graph is too large and searching all the possible paths in it would take years.

Our problem is similar to finding an Euler path in a graph, but we can’t visit all the possible edges in our case. But we can try to modify the algorithm used for an Euler path to search for our longest path.

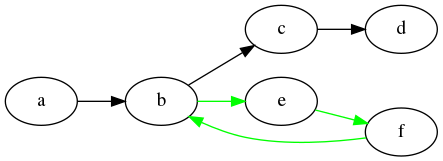
Let’s just start with any sequence. Find a node in the sequence that still has some outgoing edges that weren’t used in the sequence. If this edge can be extended to a path that doesn’t use any of the already used edges and leads back to the selected node, we can extend our sequence by this path. See the picture for an example: the sequence (a b c d) can be extended to (a b e f b c d).

Trying all the possibilities would still take ages, but we can start from a random sequence and try to extend it. This doesn’t necessarily lead to the best solution, but I’ve discovered several sequences of length 54 this way. For example

 machamp petilil landorus seaking girafarig girafarig
 gabite emboar rufflet trapinch heatmor relicanth heatmor registeel
 landorus simisear registeel lunatone emboar remoraid darmanitan
 nosepass seaking gulpin nosepass snivy yamask kangaskhan nosepass
 scrafty yamask kricketune emboar registeel lumineon nosepass simisear
 relicanth haxorus simisear rufflet tyrogue exeggcute exeggcute emboar
 relicanth heatran nosepass silcoon nosepass spoink kricketune emolga
 audino

It took about 10 to 15 minutes to discover a sequence of length 54. I had several instances of the program running for hours. The program itself is not included here, as I didn’t have time to make it pretty. Maybe if we make this a future challenge *wink*…?

Chaocipher

The description of the cipher is insufficient in the linked Wikipedia page. Fortunately, the page itself links to Moshe Rubin’s article Chaocipher Revealed: The Algorithm that describes the algorithm in detail (and even contains a Perl implementation as an appendix!) and even contains a simple example we can use to test our implementation.

I implemented the machine as a Moo object. The initial state of its disks is stored in the pt and ct attributes, but as the disks rotate, their current position is stored in private attributes. After encoding or decoding a message, the machine returns to the initial state.

#!/usr/bin/perl
use warnings;
use strict;

{   package Chaocipher;
    use Moo;

    has [qw[ pt ct ]]        => (is => 'ro');
    has [qw[ _pt _ct _pos ]] => (is => 'rw');

    sub BUILD { shift->rewind }

    sub rewind {
        my ($self) = @_;
        $self->_ct($self->ct);
        $self->_pt($self->pt);
    }

    sub _get_letter {
        my ($self, $letter, $is_plain) = @_;
        $self->_pos(index $self->${\ qw( _pt _ct )[$is_plain] },
                    $letter);
        return substr $self->${\ qw( _ct _pt )[$is_plain] },
                      $self->_pos, 1
    }

    sub _rotate {
        my ($self, $is_plain) = @_;
        my $cp = $self->${\ qw( _ct _pt )[$is_plain] };
        $cp .= substr $cp, 0, $self->_pos, "";
        $cp .= substr $cp, 0, 1, "" if $is_plain;
        substr $cp, 13, 0, substr $cp, 1 + $is_plain, 1, "";
        return $cp
    }

    sub encode {
        my ($self, $text, $is_plain) = @_;
        $is_plain ||= 0;
        my $cipher_text = "";
        for my $i (0 .. length($text) - 1) {
            my $letter = substr $text, $i, 1;
            $cipher_text .= $self->_get_letter($letter, $is_plain);
            $self->_ct($self->_rotate(0));
            $self->_pt($self->_rotate(1));
        }
        $self->rewind;
        return $cipher_text
    }

    sub decode {
        my ($self, $text) = @_;
        return $self->encode($text, 1)
    }

}

use Test::More tests => 4;

my $ch = 'Chaocipher'->new(
    pt => 'PTLNBQDEOYSFAVZKGJRIHWXUMC',
    ct => 'HXUCZVAMDSLKPEFJRIGTWOBNYQ',
);

is $ch->encode('A'), 'P', 'single letter encoded';
is $ch->encode('WELLDONEISBETTERTHANWELLSAID'),
               'OAHQHCNYNXTSZJRRHJBYHQKSOUJY',
    'long text encoded';

is $ch->decode('P'), 'A', 'single letter decoded';
is $ch->decode('OAHQHCNYNXTSZJRRHJBYHQKSOUJY'),
               'WELLDONEISBETTERTHANWELLSAID',
    'long text decoded';

What’s nice about the cipher is how both the disks behave similarly: there’s just one subroutine to rotate them both, to read the current letter from them, and even the decoding and encoding work basically the same.