E. Choroba

The Task

We’re given a grid with obstacles, we’re supposed to count all the reachable plots in the grid in a given number of steps (we can only move one plot at a time horizontally or vertically).

The sample input looks like this:

...........
.....###.#.
.###.##..#.
..#.#...#..
....#.#....
.##..S####.
.##..#...#.
.......##..
.##.#.####.
.##..##.##.
...........

where S is the starting position.

Part 1

In the first part, we should count the plots reachable in 64 steps. I went with a non-recursive solution using a stack of positions to visit.

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

my ($sy, $sx);
my @garden;
while (<>) {
    chomp;
    push @garden, [split //];
    ($sy, $sx) = ($. - 1, pos($_) - 1) if /S/g;
}
$garden[$sy][$sx] = '.';

my @MOVES = ([0, 1], [0, -1], [1, 0], [-1, 0]);
my @agenda = ([$sy, $sx]);
my $reach = 0;
for (1 .. 64) {
    my %next;
    for my $pos (@agenda) {
        my ($y, $x) = @$pos;

        for my $move (@MOVES) {
            my ($ny, $nx) = ($y + $move->[0], $x + $move->[1]);
            undef $next{$ny}{$nx} if $ny >= 0 && $ny <= $#garden
                                  && $nx >= 0 && $nx <= $#{ $garden[0] }
                                  && $garden[$ny][$nx] eq '.';
        }
    }
    @agenda = ();
    for my $y (keys %next) {
        for my $x (keys %{ $next{$y} }) {
            push @agenda, [$y, $x];
        }
    }
}

say scalar @agenda;

Part 2

The twist in the second part is subtle but it has colossal consequences. Whenever we try to go outside the grid, the grid is expanded with the exact copy of the original grid in the required direction. The number of steps we should take also changes: instead of 64, we’re supposed to take 26,501,365 steps.

We could modify the algorithm from the part 1 to expand the grid, but its performance would be horrible. We’d have to wait for years to get the answer, but to compete on the global leaderboard, we need seconds (or minutes for the local one).

I generated the output of such a modified algorithm for the first 500 steps to see whether I can detect anything that would help me with the optimisation. Plotting the graph with gnuplot yielded an increasing function for both the sample and real input data:

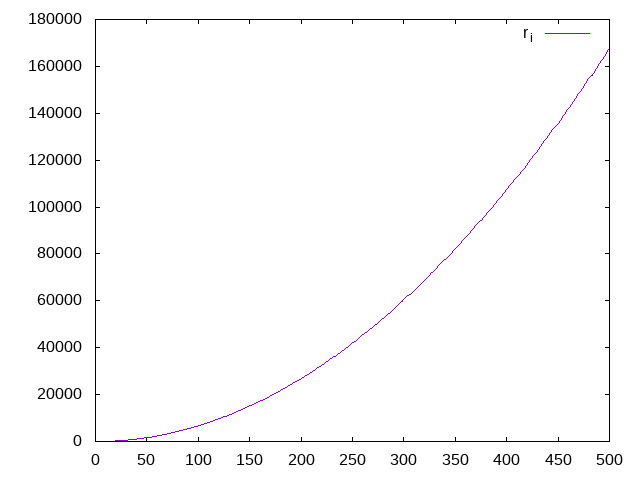
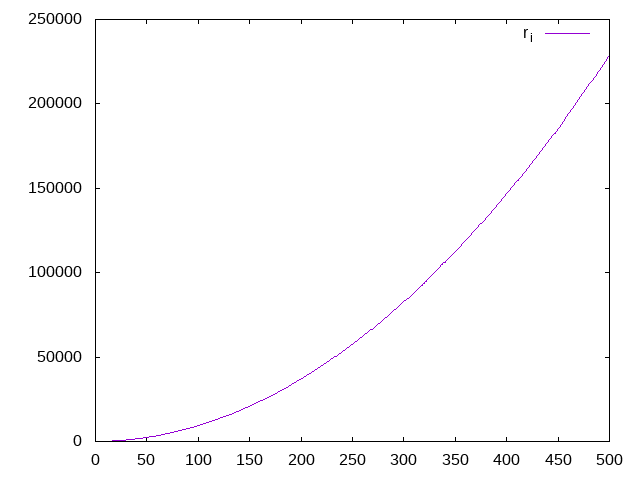
I don’t know why, but what I tried next was to plot the differences between neighbouring numbers, in a way making it possible to study the derivative of the function. The graphs are significantly different to the previous ones:

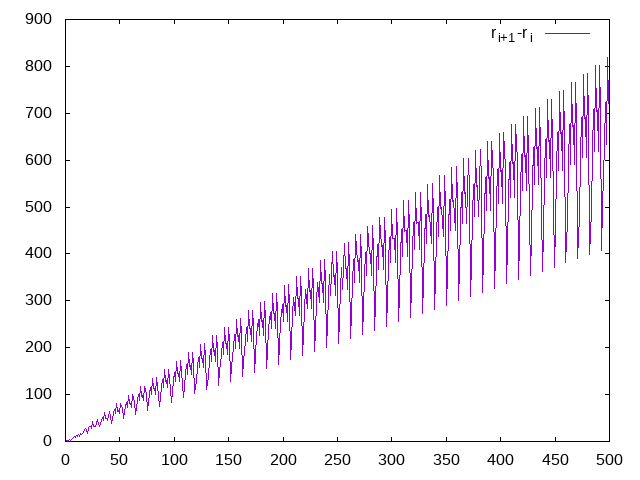
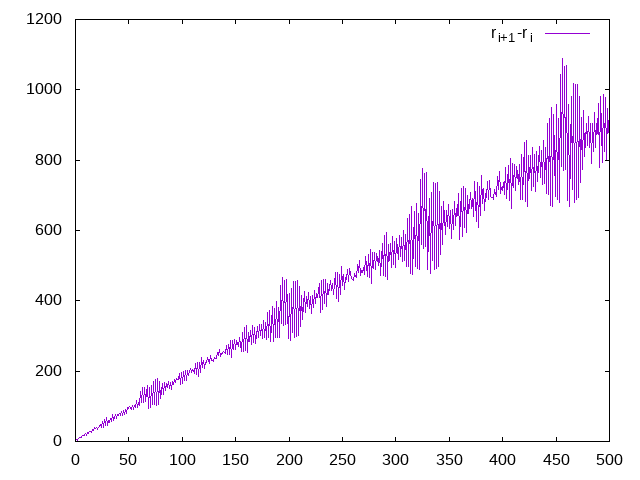
It seems there are repeated patterns, even if their amplitude is different. To see whether they’re regular, I measured the period of the repetition in the graph by hand and tried to extract each part of the pattern as a separate variable. The first element of the pattern is one line, the second element of the pattern is one line, etc.

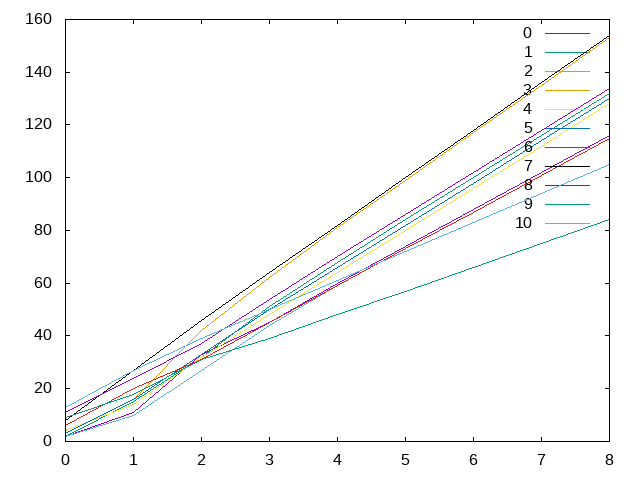
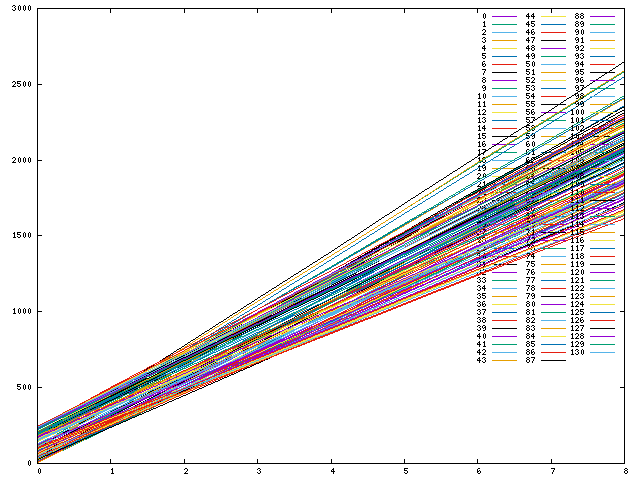
To my delight, all the lines seemed to be straight, disregarding some curving at the very beginning before the system stabilised.

The rest of the work was routine, basically just implementing the same process. At first, I had no idea how to implement the measurement of the period, but in the end, it was straightforward: the program tries all the possible periods from 2, if the period is applicable to all the parts of the pattern, we’re done.

Once we know the period, we can easily generate the next element in the sequence. As generating 26 million elements still takes some time, we can calculate the result instead. The main trick is sum(1 .. x) = x * (x + 1) / 2.

#!/usr/bin/perl
use warnings;
use strict;
use feature qw{ say };

my $TARGET = 26501365;

my ($sy, $sx);
my @garden;
while (<>) {
    chomp;
    push @garden, [split //];
    ($sy, $sx) = ($. - 1, pos($_) - 1) if /S/g;
}
$garden[$sy][$sx] = '.';

my @MOVES = ([0, 1], [0, -1], [1, 0], [-1, 0]);
my %ACCESS;
for my $y (0 .. $#garden) {
    for my $x (0 .. $#{ $garden[0] }) {
        for my $move (@MOVES) {
            my ($ny, $nx) = ($y + $move->[0], $x + $move->[1]);
            push @{ $ACCESS{$y}{$x} }, $move
                if '.' eq $garden[ $ny % @garden ][ $nx % @{ $garden[0] } ];
        }
    }
}

my @reach = (0);
my @diff;
my @agenda = ([$sy, $sx]);
my $period = 0;

my $i = 0;
EXPANSION:
while (! $period) {
    ++$i;
    say "Expanding to $i";
    my %next;
    for my $pos (@agenda) {
        my ($y, $x) = @$pos;

        for my $move (@{ $ACCESS{ $y % @garden }{ $x % @{ $garden[0] } } }) {
            my $ny = $y + $move->[0];
            my $nx = $x + $move->[1];
            undef $next{$ny}{$nx}
        }
    }
    @agenda = ();
    for my $y (keys %next) {
        for my $x (keys %{ $next{$y} }) {
            push @agenda, [$y, $x];
        }
    }
    $reach[$i] = @agenda;
    $diff[$i]  = $reach[$i] - $reach[ $i - 1 ];

    next if $i % 50 != 0;  # Search for the period only sometimes.

  PERIOD:
    for my $p (2 .. $i / 3 - 1) {
        say "Trying period $p at size $i.";
        for my $from ($i - $p .. $i) {
            next PERIOD
                if $diff[$from] - $diff[ $from - $p ]
                   != $diff[ $from - $p ] - $diff[ $from - 2 * $p ];
        }
        last PERIOD unless $p;

        say "Found $p";

        # Extend the data so we can calculate the result.
        while ($i++ < 6 * $p) {
            $diff[$i] = 2 * $diff[ $i - $p ] - $diff[ $i - 2 * $p ];
            $reach[$i] = $reach[ $i - 1 ] + $diff[ $i ];
        }

        $period = $p;
        last EXPANSION
    }
}

my (@d, @d2);
for my $i (0 .. $period - 1) {
    $d2[$i] = $diff[ $i + 5 * $period ] - $diff[ 4 * $period + $i ];
    $d[$i]  = $diff[4 * $period + $i] - 4 * $d2[$i];
}

my $m = $TARGET % $period;

my $d = 0;
my $d2 = 0;
for my $j (3 * $period + $m + 1 .. 4 * $period + $m) {
    my $dd = $d[$j % $period] + $d2[$j % $period] * (1 + int($j / $period));
    $d += $dd;
    $d2 += $d2[$j % $period];
}

my $n = int(($TARGET - 4 * $period - $m - 1)/ $period) + 1;
my $s = $reach[ 4 * $period + $m ] + $d * $n + $d2 * ($n * ($n - 1) / 2);
say $s;